题目内容
 如图,AB=AC,AE=AF,求证:点D在∠BAC的平分线上.
如图,AB=AC,AE=AF,求证:点D在∠BAC的平分线上.考点:全等三角形的判定与性质
专题:
分析:连接BC,可先证明△ABE≌△ACF,可得∠ACD=∠ABD,结合条件可得∠DCB=∠DBC,可证得CD=BD,可知AD垂直平分BC,由等腰三角形的性质可知证得结论.
解答: 证明:如图,连接BC,
证明:如图,连接BC,
在△ABE和△ACF中,
∴△ABE≌△ACF(SAS),
∴∠ACD=∠ABD,
又∵AB=AC,
∴∠ACB=∠ABC,
∴∠DCB=∠DBC,
∴DC=DB,
∴AD垂直平分BC,
又∵AC=AB,
∴AD平分∠A,
即点D在∠BAC的平分线上.
 证明:如图,连接BC,
证明:如图,连接BC,在△ABE和△ACF中,
|
∴△ABE≌△ACF(SAS),
∴∠ACD=∠ABD,
又∵AB=AC,
∴∠ACB=∠ABC,
∴∠DCB=∠DBC,
∴DC=DB,
∴AD垂直平分BC,
又∵AC=AB,
∴AD平分∠A,
即点D在∠BAC的平分线上.
点评:本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
相关题目
 如图:⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连结FC,若正方形边长为1,求弦FC的长.
如图:⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连结FC,若正方形边长为1,求弦FC的长. 如图所示,AB是⊙O的切线,切点为B,AO交⊙O于点C,过C点的切线交AB于点D.若AD=3BD,CD=2,求⊙O的半径.
如图所示,AB是⊙O的切线,切点为B,AO交⊙O于点C,过C点的切线交AB于点D.若AD=3BD,CD=2,求⊙O的半径.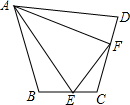 如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=
如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF=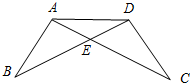 在一次数学课上,王老师在黑板上画出一幅图,并写下了四个等式:
在一次数学课上,王老师在黑板上画出一幅图,并写下了四个等式: