题目内容
 如图,已知抛物线y=-x2+bx+c与x轴交于点A(-2,0)、B(4,0),点C是这个抛物线上一点且点C在第一象限,点D是OC的中点,联结BD并延长交AC于点E.
如图,已知抛物线y=-x2+bx+c与x轴交于点A(-2,0)、B(4,0),点C是这个抛物线上一点且点C在第一象限,点D是OC的中点,联结BD并延长交AC于点E.(1)求这个抛物线的解析式;
(2)求
| CE |
| AE |
(3)当tan∠CAB=2时,求△CDE的面积.
考点:二次函数综合题
专题:综合题
分析:(1)将点A、点B的坐标代入抛物线解析式,利用待定系数法可求出这个抛物线的解析式;
(2)过点O作OH∥AC交BE于点H,根据A、B的坐标可得OA=2,OB=4,AB=6,证明OH=CE,将根据
=
=
,可得出答案;
(3)过点C作CF⊥AB,垂足为点F,设C(x,-x2+2x+8),则F(x,0),根据tan∠CAB=2,解出x的值,得出点C的坐标,求出△ABC的面积,连接OE,设S△CDE=y,表示出△OCE,△OAE,△OAC的面积,继而可求出y的值.
(2)过点O作OH∥AC交BE于点H,根据A、B的坐标可得OA=2,OB=4,AB=6,证明OH=CE,将根据
| CE |
| AE |
| OH |
| AE |
| BO |
| BA |
(3)过点C作CF⊥AB,垂足为点F,设C(x,-x2+2x+8),则F(x,0),根据tan∠CAB=2,解出x的值,得出点C的坐标,求出△ABC的面积,连接OE,设S△CDE=y,表示出△OCE,△OAE,△OAC的面积,继而可求出y的值.
解答:解:(1)∵抛物线y=-x2+bx+c过点A(-2,0)、B(4,0),
∴
,
解得:
,
∴y=-x2+2x+8.
 (2)过点O作OH∥AC交BE于点H,
(2)过点O作OH∥AC交BE于点H,
∵A(-2,0)、B(4,0),
∴OA=2,OB=4,AB=6,
∵D是OC的中点,
∴CD=OD,
∵OH∥AC,
∴
=
=1,
∴OH=CE,
∴
=
=
,
∴
=
.
 (3)过点C作CF⊥AB,垂足为点F,
(3)过点C作CF⊥AB,垂足为点F,
设C(x,-x2+2x+8),则F(x,0),
∴AF=x+2,CF=-x2+2x+8,
∵在Rt△AFC中,tan∠CAB=
=2,
∴
=2,
解得:x=2,
∴C(2,8),
∴S△AOC=
×2×8=8,
连接OE,设S△CDE=y,
∵OD=CD,
∴S△ODE=S△CDE=y,
∴S△OCE=2y,
∵
=
,
∴
=
,
∴S△OAE=3y,
∴S△OAC=5y,
∴5y=8,
∴y=
.
∴△CDE的面积为
.
∴
|
解得:
|
∴y=-x2+2x+8.
 (2)过点O作OH∥AC交BE于点H,
(2)过点O作OH∥AC交BE于点H,∵A(-2,0)、B(4,0),
∴OA=2,OB=4,AB=6,
∵D是OC的中点,
∴CD=OD,
∵OH∥AC,
∴
| OH |
| CE |
| OD |
| CD |
∴OH=CE,
∴
| CE |
| AE |
| OH |
| AE |
| BO |
| BA |
∴
| CE |
| AE |
| 2 |
| 3 |
 (3)过点C作CF⊥AB,垂足为点F,
(3)过点C作CF⊥AB,垂足为点F,设C(x,-x2+2x+8),则F(x,0),
∴AF=x+2,CF=-x2+2x+8,
∵在Rt△AFC中,tan∠CAB=
| CF |
| AF |
∴
| -x2+2x+8 |
| x+2 |
解得:x=2,
∴C(2,8),
∴S△AOC=
| 1 |
| 2 |
连接OE,设S△CDE=y,
∵OD=CD,
∴S△ODE=S△CDE=y,
∴S△OCE=2y,
∵
| CE |
| AE |
| 2 |
| 3 |
∴
| S△OCE |
| S△AOE |
| 2 |
| 3 |
∴S△OAE=3y,
∴S△OAC=5y,
∴5y=8,
∴y=
| 8 |
| 5 |
∴△CDE的面积为
| 8 |
| 5 |
点评:本题考查了二次函数的综合,涉及了待定系数法求函数解析式、三角形的面积及锐角三角函数的定义,综合性较强,解答此类综合性题目,关键是数形结合思想的运用,难度较大.

练习册系列答案
相关题目
 如图,将矩形ABCD沿CE向上折叠,使点B落在AD边上的点F处.若AE=
如图,将矩形ABCD沿CE向上折叠,使点B落在AD边上的点F处.若AE=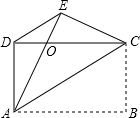 如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.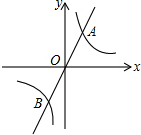 如图,直线y=mx与双曲线y=
如图,直线y=mx与双曲线y=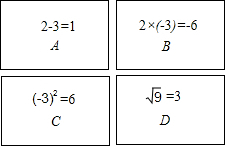 如图,有四张卡片(形状、大小和质地都相同),正面分别写有字母A、B、C、D和一个不同的算式,将这四张卡片背面向上洗匀,从中随机抽取两张卡片,这两张卡片上的算式只有一个正确的概率是
如图,有四张卡片(形状、大小和质地都相同),正面分别写有字母A、B、C、D和一个不同的算式,将这四张卡片背面向上洗匀,从中随机抽取两张卡片,这两张卡片上的算式只有一个正确的概率是