题目内容
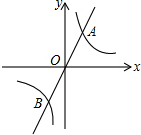 如图,直线y=mx与双曲线y=
如图,直线y=mx与双曲线y=| k |
| x |
(1)求反比例函数的表达式;
(2)根据图象直接写出当mx>
| k |
| x |
(3)计算线段AB的长.
考点:反比例函数与一次函数的交点问题
专题:数形结合,待定系数法
分析:(1)把A的坐标代入反比例函数的解析式即可求出答案;
(2)求出直线的解析式,解组成的方程组求出B的坐标,根据A、B的坐标结合图象即可得出答案;
(3)根据A、B的坐标.利用勾股定理分别求出OA、OB,即可得出答案.
(2)求出直线的解析式,解组成的方程组求出B的坐标,根据A、B的坐标结合图象即可得出答案;
(3)根据A、B的坐标.利用勾股定理分别求出OA、OB,即可得出答案.
解答: 解:(1)把A(1,2)代入y=
解:(1)把A(1,2)代入y=
得:k=2,
即反比例函数的表达式是y=
;
(2)把A(1,2)代入y=mx得:m=2,
即直线的解析式是y=2x,
解方程组
得出B点的坐标是(-1,-2),
∴当mx>
时,x的取值范围是-1<x<0或x>1;
(3)过A作AC⊥x轴于C,
∵A(1,2),
∴AC=2,OC=1,
由勾股定理得:AO=
=
,
同理求出OB=
,
∴AB=2
.
 解:(1)把A(1,2)代入y=
解:(1)把A(1,2)代入y=| k |
| x |
即反比例函数的表达式是y=
| 2 |
| x |
(2)把A(1,2)代入y=mx得:m=2,
即直线的解析式是y=2x,
解方程组
|
∴当mx>
| k |
| x |
(3)过A作AC⊥x轴于C,
∵A(1,2),
∴AC=2,OC=1,
由勾股定理得:AO=
| 22+12 |
| 5 |
同理求出OB=
| 5 |
∴AB=2
| 5 |
点评:本题考查了一次函数和反比例函数的交点问题,用待定系数法求函数的解析式的应用,主要考查学生的理解能力和观察图象的能力,题目比较典型,难度不大.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
等腰三角形一条边的边长为3,它的另两条边的边长是关于x的一元二次方程x2-12x+k=0的两个根,则k的值是( )
| A、27 | B、36 |
| C、27或36 | D、18 |
 如图,已知抛物线y=-x2+bx+c与x轴交于点A(-2,0)、B(4,0),点C是这个抛物线上一点且点C在第一象限,点D是OC的中点,联结BD并延长交AC于点E.
如图,已知抛物线y=-x2+bx+c与x轴交于点A(-2,0)、B(4,0),点C是这个抛物线上一点且点C在第一象限,点D是OC的中点,联结BD并延长交AC于点E.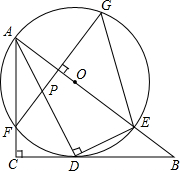 如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交⊙O于G,连接GE.
如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交⊙O于G,连接GE.