题目内容
 如图,将矩形ABCD沿CE向上折叠,使点B落在AD边上的点F处.若AE=
如图,将矩形ABCD沿CE向上折叠,使点B落在AD边上的点F处.若AE=| 2 |
| 3 |
考点:翻折变换(折叠问题),勾股定理,矩形的性质
专题:数形结合,转化思想
分析:由AE=
BE,可设AE=2k,则BE=3k,AB=5k.由四边形ABCD是矩形,可得∠A=∠ABC=∠D=90°,CD=AB=5k,AD=BC.由折叠的性质可得∠EFC=∠B=90°,EF=EB=3k,CF=BC,由同角的余角相等,即可得∠DCF=∠AFE.在Rt△AEF中,根据勾股定理求出AF=
=
k,由cos∠AFE=cos∠DCF得出CF=3
k,即AD=3
k,进而求解即可.
| 2 |
| 3 |
| EF2-AE2 |
| 5 |
| 5 |
| 5 |
解答:解:∵AE=
BE,
∴设AE=2k,则BE=3k,AB=5k.
∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=90°,CD=AB=5k,AD=BC.
∵将矩形ABCD沿CE向上折叠,使点B落在AD边上的点F处,
∴∠EFC=∠B=90°,EF=EB=3k,CF=BC,
∴∠AFE+∠DFC=90°,∠DFC+∠FCD=90°,
∴∠DCF=∠AFE,
∴cos∠AFE=cos∠DCF.
在Rt△AEF中,
∵∠A=90°,AE=2k,EF=3k,
∴AF=
=
k,
∴
=
,即
=
,
∴CF=3
k,
∴AD=BC=CF=3
k,
∴长AD与宽AB的比值是
=
.
故答案为:
.
| 2 |
| 3 |
∴设AE=2k,则BE=3k,AB=5k.
∵四边形ABCD是矩形,
∴∠A=∠ABC=∠D=90°,CD=AB=5k,AD=BC.
∵将矩形ABCD沿CE向上折叠,使点B落在AD边上的点F处,
∴∠EFC=∠B=90°,EF=EB=3k,CF=BC,
∴∠AFE+∠DFC=90°,∠DFC+∠FCD=90°,
∴∠DCF=∠AFE,
∴cos∠AFE=cos∠DCF.
在Rt△AEF中,
∵∠A=90°,AE=2k,EF=3k,
∴AF=
| EF2-AE2 |
| 5 |
∴
| AF |
| EF |
| CD |
| CF |
| ||
| 3k |
| 5k |
| CF |
∴CF=3
| 5 |
∴AD=BC=CF=3
| 5 |
∴长AD与宽AB的比值是
3
| ||
| 5k |
3
| ||
| 5 |
故答案为:
3
| ||
| 5 |
点评:此题考查了折叠的性质,矩形的性质,勾股定理以及三角函数的定义.解此题的关键是数形结合思想与转化思想的应用.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
等腰三角形一条边的边长为3,它的另两条边的边长是关于x的一元二次方程x2-12x+k=0的两个根,则k的值是( )
| A、27 | B、36 |
| C、27或36 | D、18 |
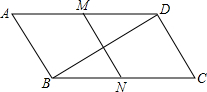 如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.
如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD. 如图,在Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AC于点E.∠A=30°,AB=8,则DE的长度是
如图,在Rt△ABC中,∠C=90°,D为AB的中点,DE⊥AC于点E.∠A=30°,AB=8,则DE的长度是 已知如图:△ABC、△DCE均为等腰直角三角形,其中AC=BC,DC=DE,∠ACB=∠D=90°,将△DCE绕点C旋转,两边分别交AB于M、N.若AM=3,BN=4,则△CMN的面积为
已知如图:△ABC、△DCE均为等腰直角三角形,其中AC=BC,DC=DE,∠ACB=∠D=90°,将△DCE绕点C旋转,两边分别交AB于M、N.若AM=3,BN=4,则△CMN的面积为 如图,在等腰三角形纸片ABC中,AB=AC,∠A=50°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE=
如图,在等腰三角形纸片ABC中,AB=AC,∠A=50°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE= 如图,已知抛物线y=-x2+bx+c与x轴交于点A(-2,0)、B(4,0),点C是这个抛物线上一点且点C在第一象限,点D是OC的中点,联结BD并延长交AC于点E.
如图,已知抛物线y=-x2+bx+c与x轴交于点A(-2,0)、B(4,0),点C是这个抛物线上一点且点C在第一象限,点D是OC的中点,联结BD并延长交AC于点E.