题目内容
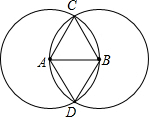 如图,分别为线段AB的两个端点A、B为圆心,以线段AB为半径画圆,两圆交于C、D两点,则下列判断中正确的是( )
如图,分别为线段AB的两个端点A、B为圆心,以线段AB为半径画圆,两圆交于C、D两点,则下列判断中正确的是( )| A、△ABC和△ABD都一定是等边三角形 |
| B、△ABC和△ABD都不一定是等边三角形 |
| C、△ABC不一定是等边三角形 |
| D、△ABD不一定是等边三角形 |
考点:相交两圆的性质
专题:
分析:根据同一个圆的半径都相等即可证得.
解答:解:∵BC和BA都是⊙B的半径,
∴BC=AB,
又∵AB和AC都是⊙A的半径,
∴AC=AB,
∴AC=AB=BC,即△ABC是等边三角形,
同理,△ABD是等边三角形.
故选A.
∴BC=AB,
又∵AB和AC都是⊙A的半径,
∴AC=AB,
∴AC=AB=BC,即△ABC是等边三角形,
同理,△ABD是等边三角形.
故选A.
点评:本题考查了等边三角形的定义,以及圆的定义,理解圆的定义是关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
圆绕着某一点旋转任意角度都能与自身重合,这一点是( )
| A、圆心 | B、点O |
| C、圆内任意一点 | D、圆上任意一点 |
直线m外的一点P,它到直线m上三点A,B,C的距离分别是6cm,3cm,5cm,则点P到直线m的距离为( )
| A、3cm | B、5cm |
| C、6cm | D、不大于3cm |
 如图,已知AB是⊙O的直径,弦AC平分∠BAM且CD⊥AM于D,点I是△ABC的内心,连接CI并延长交⊙O于E,连接AE.
如图,已知AB是⊙O的直径,弦AC平分∠BAM且CD⊥AM于D,点I是△ABC的内心,连接CI并延长交⊙O于E,连接AE.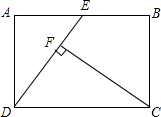 已知:如图,在矩形ABCD中,E是AB上的中点,CF⊥DE于F,若AD=8,AB=12.求CF的长.
已知:如图,在矩形ABCD中,E是AB上的中点,CF⊥DE于F,若AD=8,AB=12.求CF的长.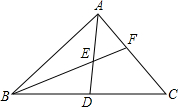 若D为△ABC边BC的中点,E为AD的中点,BE交AC于点F,则AF:FC=
若D为△ABC边BC的中点,E为AD的中点,BE交AC于点F,则AF:FC=
 已知:E是正方形ABCD的边长AD上一点,BF平分∠EBC,交CD于F,求证:BE=AE+CF.
已知:E是正方形ABCD的边长AD上一点,BF平分∠EBC,交CD于F,求证:BE=AE+CF.