题目内容
 如图,已知AB是⊙O的直径,弦AC平分∠BAM且CD⊥AM于D,点I是△ABC的内心,连接CI并延长交⊙O于E,连接AE.
如图,已知AB是⊙O的直径,弦AC平分∠BAM且CD⊥AM于D,点I是△ABC的内心,连接CI并延长交⊙O于E,连接AE.(1)求证:CD是⊙O的切线;
(2)求证:AE=DE;
(3)若AD=
| 32 |
| 5 |
考点:切线的判定
专题:证明题
分析:(1)连结OC,如图1,由AC平分∠BAM得到∠1=∠2,加上∠2=∠3,则∠1=∠3,于是可判断OC∥AD,由于AD⊥CD,所以OC⊥AD,然后根据切线的判定定理即可得到CD是⊙O的切线;
(2)连结AI、CB,如图2,由三角形内心的定义得到∠CAI=∠BAI,∠ACE=∠BCE,再利用三角形外角性质得∠AIE=∠ACB+∠CAI=∠BCE+∠BAI,而∠BCE=∠BAE,所以∠AIE=∠BAE+∠BAI,即∠AIE=∠EAI,于是根据等腰三角形的判定得AE=IE;
(3)作EM⊥AC于M,EN⊥BC于N,如图3,根据圆周角定理,由AB为直径得到∠ACB=90°,加上DAC=∠CAB,则可判断Rt△ADC∽Rt△ACB,利用相似比可计算出AB=10,再利用勾股定理计算出BC=6,接着证明Rt△AEM≌Rt△BEN得到AM=BN,再利用四边形CMEN为正方形得CM=CN,所以CM=AC-AM=AC-BN=AC-(CN-BC),于是可计算出CM=
(AC+BC)=
×(6+8)=7,然后利用CE=
CM进行计算.
(2)连结AI、CB,如图2,由三角形内心的定义得到∠CAI=∠BAI,∠ACE=∠BCE,再利用三角形外角性质得∠AIE=∠ACB+∠CAI=∠BCE+∠BAI,而∠BCE=∠BAE,所以∠AIE=∠BAE+∠BAI,即∠AIE=∠EAI,于是根据等腰三角形的判定得AE=IE;
(3)作EM⊥AC于M,EN⊥BC于N,如图3,根据圆周角定理,由AB为直径得到∠ACB=90°,加上DAC=∠CAB,则可判断Rt△ADC∽Rt△ACB,利用相似比可计算出AB=10,再利用勾股定理计算出BC=6,接着证明Rt△AEM≌Rt△BEN得到AM=BN,再利用四边形CMEN为正方形得CM=CN,所以CM=AC-AM=AC-BN=AC-(CN-BC),于是可计算出CM=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
解答:(1)证明:连结OC,如图1,
∵AC平分∠BAM,
∴∠1=∠2,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥AD,
∴CD是⊙O的切线;
(2)证明: 连结AI、CB,如图2,
连结AI、CB,如图2,
∵点I是△ABC的内心,
∴AI平分∠BAC,EI平分∠ACB,
∴∠CAI=∠BAI,∠ACE=∠BCE,
∴∠AIE=∠ACB+∠CAI=∠BCE+∠BAI,
而∠BCE=∠BAE,
∴∠AIE=∠BAE+∠BAI,
即∠AIE=∠EAI,
∴AE=IE;
(3)解:作EM⊥AC于M,EN⊥BC于N,如图3,
∵AB为直径,
∴∠ACB=90°,
∵∠DAC=∠CAB,
∴Rt△ADC∽Rt△ACB,
∴
=
,即
=
,解得AB=10,
在Rt△ACB中,∵AB=10,AC=8,
∴BC=
=6,
∵CE平分∠ACB,
∴∠ACE=∠BCE=45°,
∴EM=EN,
=
,
∴AE=BE,
在Rt△AEM和Rt△BEN中,
,
∴Rt△AEM≌Rt△BEN,
∴AM=BN,
∵四边形CMEN为正方形,
∴CM=CN,
∴CM=AC-AM=AC-BN=AC-(CN-BC),
∴CM=
(AC+BC)=
×(6+8)=7,
∴CE=
CM=7
.
即AB和CE的长分别为10,7
.

∵AC平分∠BAM,
∴∠1=∠2,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥AD,
∴CD是⊙O的切线;
(2)证明:
 连结AI、CB,如图2,
连结AI、CB,如图2,∵点I是△ABC的内心,
∴AI平分∠BAC,EI平分∠ACB,
∴∠CAI=∠BAI,∠ACE=∠BCE,
∴∠AIE=∠ACB+∠CAI=∠BCE+∠BAI,
而∠BCE=∠BAE,
∴∠AIE=∠BAE+∠BAI,
即∠AIE=∠EAI,
∴AE=IE;
(3)解:作EM⊥AC于M,EN⊥BC于N,如图3,

∵AB为直径,
∴∠ACB=90°,
∵∠DAC=∠CAB,
∴Rt△ADC∽Rt△ACB,
∴
| AD |
| AC |
| AC |
| AB |
| ||
| 8 |
| 8 |
| AB |
在Rt△ACB中,∵AB=10,AC=8,
∴BC=
| AB2-AC2 |
∵CE平分∠ACB,
∴∠ACE=∠BCE=45°,
∴EM=EN,
 |
| AE |
 |
| BE |
∴AE=BE,
在Rt△AEM和Rt△BEN中,
|
∴Rt△AEM≌Rt△BEN,
∴AM=BN,
∵四边形CMEN为正方形,
∴CM=CN,
∴CM=AC-AM=AC-BN=AC-(CN-BC),
∴CM=
| 1 |
| 2 |
| 1 |
| 2 |
∴CE=
| 2 |
| 2 |
即AB和CE的长分别为10,7
| 2 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了勾股定理和相似三角形的判定与性质.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
如果y=(m-1)x2-m2+3是一次函数,那么m的值是( )
| A、1 | ||
| B、-1 | ||
| C、±1 | ||
D、±
|
已知a∥b,b∥c,则直线a与c的关系是( )
| A、相交 | B、平行 |
| C、相交或平行 | D、垂直 |
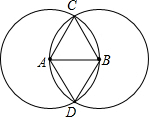 如图,分别为线段AB的两个端点A、B为圆心,以线段AB为半径画圆,两圆交于C、D两点,则下列判断中正确的是( )
如图,分别为线段AB的两个端点A、B为圆心,以线段AB为半径画圆,两圆交于C、D两点,则下列判断中正确的是( )| A、△ABC和△ABD都一定是等边三角形 |
| B、△ABC和△ABD都不一定是等边三角形 |
| C、△ABC不一定是等边三角形 |
| D、△ABD不一定是等边三角形 |
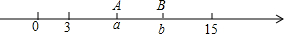 如图,一根木棒放在数轴上,木棒的左端与数轴上的数a表示的点A重合,右端与数轴b表示的点B重合,若将木棒沿数轴右方向移动,则当它的左端移动到B点时,它的右端在数轴上所对应的数为15,若将木棒沿数轴向左水平移动,则当它的右端点移动到A点时,它的左端点在数轴上所对应的数为3.
如图,一根木棒放在数轴上,木棒的左端与数轴上的数a表示的点A重合,右端与数轴b表示的点B重合,若将木棒沿数轴右方向移动,则当它的左端移动到B点时,它的右端在数轴上所对应的数为15,若将木棒沿数轴向左水平移动,则当它的右端点移动到A点时,它的左端点在数轴上所对应的数为3.