题目内容
已知线段AB=12,在线段AB上有C、D、M、N四个点,若AC:CD:DB=1:2:3,点M是AC的中点,DN=
DB,求MN的长.
| 1 |
| 3 |
考点:两点间的距离
专题:
分析:先作出图形,然后求出MN的长度.
解答:解:如图:
 ,
,
∵线段AB=12,AC:CD:DB=1:2:3,
∴AC=2,CD=4,DB=6,
∵点M是AC的中点,DN=
DB,
∴MC=1,DN=2,
∴MN=MC+CD+DN=1+4+2=7.
 ,
,∵线段AB=12,AC:CD:DB=1:2:3,
∴AC=2,CD=4,DB=6,
∵点M是AC的中点,DN=
| 1 |
| 3 |
∴MC=1,DN=2,
∴MN=MC+CD+DN=1+4+2=7.
点评:本题考查了两点间的距离,解答本题的关键是根据题意求出AC、CD、DB的长度,难度一般.

练习册系列答案
相关题目
下列四个图形中,是中心对称图形的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
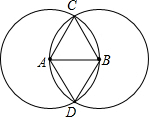 如图,分别为线段AB的两个端点A、B为圆心,以线段AB为半径画圆,两圆交于C、D两点,则下列判断中正确的是( )
如图,分别为线段AB的两个端点A、B为圆心,以线段AB为半径画圆,两圆交于C、D两点,则下列判断中正确的是( )| A、△ABC和△ABD都一定是等边三角形 |
| B、△ABC和△ABD都不一定是等边三角形 |
| C、△ABC不一定是等边三角形 |
| D、△ABD不一定是等边三角形 |
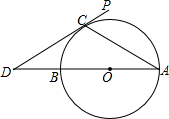 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,若OB=BD,则∠A的大小是( )
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,若OB=BD,则∠A的大小是( )| A、30° | B、32° |
| C、34° | D、36° |
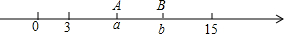 如图,一根木棒放在数轴上,木棒的左端与数轴上的数a表示的点A重合,右端与数轴b表示的点B重合,若将木棒沿数轴右方向移动,则当它的左端移动到B点时,它的右端在数轴上所对应的数为15,若将木棒沿数轴向左水平移动,则当它的右端点移动到A点时,它的左端点在数轴上所对应的数为3.
如图,一根木棒放在数轴上,木棒的左端与数轴上的数a表示的点A重合,右端与数轴b表示的点B重合,若将木棒沿数轴右方向移动,则当它的左端移动到B点时,它的右端在数轴上所对应的数为15,若将木棒沿数轴向左水平移动,则当它的右端点移动到A点时,它的左端点在数轴上所对应的数为3.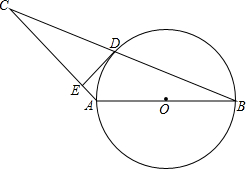 如图,在等腰△ABC中,AB=AC=5,BC=8,以一腰AB 为直径作⊙O交BC于D,又过D作DE⊥AC,垂足为E.
如图,在等腰△ABC中,AB=AC=5,BC=8,以一腰AB 为直径作⊙O交BC于D,又过D作DE⊥AC,垂足为E.