题目内容
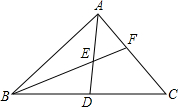 若D为△ABC边BC的中点,E为AD的中点,BE交AC于点F,则AF:FC=
若D为△ABC边BC的中点,E为AD的中点,BE交AC于点F,则AF:FC=考点:三角形中位线定理
专题:
分析:过D点作DG平行于AC交BF与G点,根据E为AD中点可知AE=DE 再由DG∥AC可知∠GDE=∠FAE,根据ASA定理得出△GDE≌△FAE(ASA),故可得出DG=AF,根据DG为△BCF的中位线即可得出结论.
解答: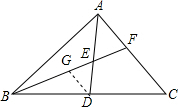 解:过D点作DG平行于AC交BF与G点,
解:过D点作DG平行于AC交BF与G点,
∵E为AD中点,
∴AE=DE
∵DG平行于AC,
∴∠GDE=∠FAE.
在△GDE与△FAE中,
∵
,
∴△GDE≌△FAE(ASA),
∴DG=AF.
∵DG为△BCF的中位线,
∴DG=
CF,
∴
=
.
故答案为:
.
 解:过D点作DG平行于AC交BF与G点,
解:过D点作DG平行于AC交BF与G点,∵E为AD中点,
∴AE=DE
∵DG平行于AC,
∴∠GDE=∠FAE.
在△GDE与△FAE中,
∵
|
∴△GDE≌△FAE(ASA),
∴DG=AF.
∵DG为△BCF的中位线,
∴DG=
| 1 |
| 2 |
∴
| AF |
| FC |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查的是三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.

练习册系列答案
相关题目
下列四个图形中,是中心对称图形的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
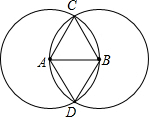 如图,分别为线段AB的两个端点A、B为圆心,以线段AB为半径画圆,两圆交于C、D两点,则下列判断中正确的是( )
如图,分别为线段AB的两个端点A、B为圆心,以线段AB为半径画圆,两圆交于C、D两点,则下列判断中正确的是( )| A、△ABC和△ABD都一定是等边三角形 |
| B、△ABC和△ABD都不一定是等边三角形 |
| C、△ABC不一定是等边三角形 |
| D、△ABD不一定是等边三角形 |
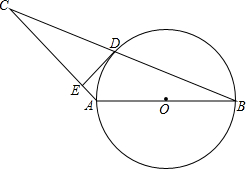 如图,在等腰△ABC中,AB=AC=5,BC=8,以一腰AB 为直径作⊙O交BC于D,又过D作DE⊥AC,垂足为E.
如图,在等腰△ABC中,AB=AC=5,BC=8,以一腰AB 为直径作⊙O交BC于D,又过D作DE⊥AC,垂足为E. 求阴影部分面积.
求阴影部分面积.