题目内容
求代数式
+
+
+…+
的值,其中,a、b满足
+(ab-2)2=0.
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2012)(b+2012) |
| a-1 |
考点:代数式求值,非负数的性质:偶次方,非负数的性质:算术平方根
专题:
分析:根据非负数的性质列式求出a、b的值,然后代入代数式,再裂项进行计算即可得解.
解答:解:由题意得,a-1=0,ab-2=0,
解得a=1,b=2,
故原式=
+
+
+…+
=1-
+
-
+
-
+…+
-
=1-
=
.
解得a=1,b=2,
故原式=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2013×2014 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2013 |
| 1 |
| 2014 |
=1-
| 1 |
| 2014 |
=
| 2013 |
| 2014 |
点评:本题考查了代数式求值,非负数的性质,根据几个非负数的和为0时,这几个非负数都为0求出a、b的值是解题的关键,难点在于把每一个算式写成两个数的差的形式.

练习册系列答案
相关题目


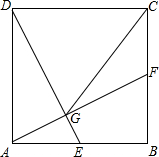 如图,在正方形ABCD中,E、F分别是边AB、BC的中点,连接AF、DE相交于点G,连接CG.
如图,在正方形ABCD中,E、F分别是边AB、BC的中点,连接AF、DE相交于点G,连接CG. 某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系如图,当总用水量达到7000米3时,该经济作物种植时间是
某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系如图,当总用水量达到7000米3时,该经济作物种植时间是