题目内容
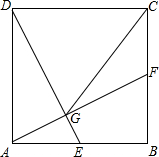 如图,在正方形ABCD中,E、F分别是边AB、BC的中点,连接AF、DE相交于点G,连接CG.
如图,在正方形ABCD中,E、F分别是边AB、BC的中点,连接AF、DE相交于点G,连接CG.(1)求证:AF⊥DE;
(2)求证:CG=CD.
考点:全等三角形的判定与性质,直角三角形的性质,正方形的性质
专题:证明题
分析:(1)正方形ABCD中,AB=BC,BF=AE,且∠ABF=∠DAE=90°,即可证明△ABF≌△DAE,即可得∠DGA=90°,结论成立.
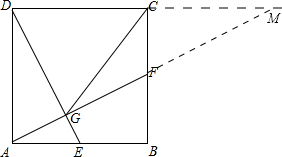
(2)延长AF交DC延长线于M,证明△ABF≌△MCF,说明△DGM是直角三角形,命题得证.
(2)延长AF交DC延长线于M,证明△ABF≌△MCF,说明△DGM是直角三角形,命题得证.
解答:证明:(1)∵四边形ABCD为正方形
∴AB=BC=CD=AD,∠ABF=∠DAE=90°,
又∵E,F分别是边AB.BC的中点
∴AE=
AB.BF=
BC
∴AE=BF.
在△ABF与△DAE中,
,
∴△DAE≌△ABF(SAS).
∴∠ADE=∠BAF,
∵∠BAF+∠DAG=90°,
∴∠ADG+∠DAG=90°,
∴∠DGA=90°,即AF⊥DE.
(2)证明:延长AF交DC延长线于M,
∵F为BC中点,
∴CF=FB
又∵DM∥AB,
∴∠M=∠FAB.
在△ABF与△MCF中,
,
∴△ABF≌△MCF(AAS),
∴AB=CM.
∴AB=CD=CM,
∵△DGM是直角三角形,
∴GC=
DM=DC.
∴AB=BC=CD=AD,∠ABF=∠DAE=90°,
又∵E,F分别是边AB.BC的中点
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=BF.
在△ABF与△DAE中,
|
∴△DAE≌△ABF(SAS).
∴∠ADE=∠BAF,
∵∠BAF+∠DAG=90°,
∴∠ADG+∠DAG=90°,
∴∠DGA=90°,即AF⊥DE.
(2)证明:延长AF交DC延长线于M,
∵F为BC中点,
∴CF=FB
又∵DM∥AB,
∴∠M=∠FAB.
在△ABF与△MCF中,
|
∴△ABF≌△MCF(AAS),
∴AB=CM.
∴AB=CD=CM,
∵△DGM是直角三角形,
∴GC=
| 1 |
| 2 |

点评:本题考查了正方形各边长相等、各内角为直角的性质,考查了全等三角形的判定和全等三角形对应角、对应边相等的性质,本题中求证△ABF≌△BCE和△ABF≌△MCF是解题的关键.

练习册系列答案
相关题目
 如图,正方形ABCD中,BC=8,将∠BAD绕着A点顺时针进行旋转,并延长∠BAD的两边分别与正方形ABCD的边CD交于点F、CB的延长线交于点E,连结EF.已知∠BAD的旋转过程中,△ADF≌△ABE.
如图,正方形ABCD中,BC=8,将∠BAD绕着A点顺时针进行旋转,并延长∠BAD的两边分别与正方形ABCD的边CD交于点F、CB的延长线交于点E,连结EF.已知∠BAD的旋转过程中,△ADF≌△ABE.