题目内容
6. 如图,△ABC是等边三角形,BD是△ABC的角平分线,交边AC于点D,EC⊥BC于点C,CE=BD.求证:△ADE是等边三角形.
如图,△ABC是等边三角形,BD是△ABC的角平分线,交边AC于点D,EC⊥BC于点C,CE=BD.求证:△ADE是等边三角形.
分析 先依据等腰三角形三线合一的性质得到AB=AC,∠ADB=90°,然后证明△ABD≌△ACE,依据全等三角形的性质可得到AD=AE,∠EAC=∠DAB=60°,最后依据有一个角等于60°的等腰三角形是等边三角形进行证明即可.
解答 证明:△ABC是等边三角形,BD是△ABC的角平分线,
∴BD⊥AC,AB=AC,∠ABD=30°,∠ACB=60°.
∵EC⊥BC,
∴∠BCE=90°,
∴∠ACE=∠ABD=30°.
在△ABD和△ACE中,$\left\{\begin{array}{l}{BD=CE}\\{∠EAC=∠DAB}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△ACE.
∴AD=AE,∠EAC=∠DAB=60°.
∴△ADE是等边三角形.
点评 本题主要考查的是等边三角形的性质和判定、等腰三角形的性质、全等三角形的性质和判定,熟练掌握相关性质和判定定理是解题的关键.

练习册系列答案
相关题目
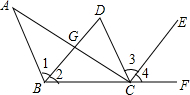 如图,CD∥AB,BD平分∠ABC,CE平分∠DCF,∠ACE=90°
如图,CD∥AB,BD平分∠ABC,CE平分∠DCF,∠ACE=90°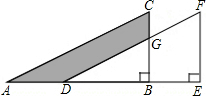 如图,将直角三角形ABC沿AB方向平移AD长的距离得到直角三角形DEF,已知BE=5,EF=8,CG=3.则图中阴影部分面积$\frac{65}{2}$.
如图,将直角三角形ABC沿AB方向平移AD长的距离得到直角三角形DEF,已知BE=5,EF=8,CG=3.则图中阴影部分面积$\frac{65}{2}$.