题目内容
15.先化简,再求值:$\frac{{x}^{2}-9}{{x}^{2}+6x+9}$-$\frac{x}{x+3}$,其中x=4.分析 根据分式的减法可以化简题目中的式子,然后将x的值代入即可解答本题.
解答 解:$\frac{{x}^{2}-9}{{x}^{2}+6x+9}$-$\frac{x}{x+3}$
=$\frac{(x+3)(x-3)}{(x+3)^{2}}-\frac{x}{x+3}$
=$\frac{x-3}{x+3}-\frac{x}{x+3}$
=$-\frac{3}{x+3}$,
当x=4时,原式=$-\frac{3}{4+3}=-\frac{3}{7}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
相关题目
5.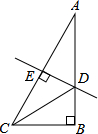 如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=3,则AB的长是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=3,则AB的长是( )
 如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=3,则AB的长是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=3,则AB的长是( )| A. | 9 | B. | 6$\sqrt{3}$ | C. | 6 | D. | 3$\sqrt{3}$ |
 如图,△ABC是等边三角形,BD是△ABC的角平分线,交边AC于点D,EC⊥BC于点C,CE=BD.求证:△ADE是等边三角形.
如图,△ABC是等边三角形,BD是△ABC的角平分线,交边AC于点D,EC⊥BC于点C,CE=BD.求证:△ADE是等边三角形.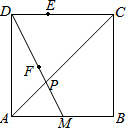 如图,正方形ABCD中,BC=2,点M是边AB的中点,连接DM,DM与AC交于点P,点E在DC上,点F在DP上,且∠DFE=45°.若PF=$\frac{\sqrt{5}}{6}$,则CE=$\frac{7}{6}$.
如图,正方形ABCD中,BC=2,点M是边AB的中点,连接DM,DM与AC交于点P,点E在DC上,点F在DP上,且∠DFE=45°.若PF=$\frac{\sqrt{5}}{6}$,则CE=$\frac{7}{6}$.
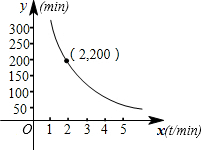 码头工人往一艘轮船上装载货物,装完货物所需时间ymin与装载速度xt/min之间的函数关系如图.
码头工人往一艘轮船上装载货物,装完货物所需时间ymin与装载速度xt/min之间的函数关系如图.