Question

11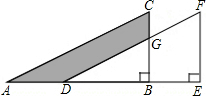．如图，将直角三角形ABC沿AB方向平移AD长的距离得到直角三角形DEF，已知BE=5，EF=8，CG=3．则图中阴影部分面积$\frac{65}{2}$．

Answer 1

分析 根据平移的性质可得△DEF≌△ABC，S_△DEF=S_△ABC，则阴影部分的面积=梯形BEFG的面积，再根据梯形的面积公式即可得到答案．

解答 解：∵RT△ABC沿AB的方向平移AD距离得△DEF，
∴△DEF≌△ABC，
∴EF=BC=8，S_△DEF=S_△ABC，
∴S_△ABC-S_△DBG=S_△DEF-S_△DBG，
∴S_{四边形ACGD}=S_梯形BEFG，
∵CG=3，
∴BG=BC-CG=8-3=5，
∴S_梯形BEFG=$\frac{1}{2}$（BG+EF）•BE=$\frac{1}{2}$（5+8）×5=$\frac{65}{2}$．
故答案为：$\frac{65}{2}$．

点评 本题考查了平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同． ②新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行且相等．