题目内容
17.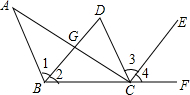 如图,CD∥AB,BD平分∠ABC,CE平分∠DCF,∠ACE=90°
如图,CD∥AB,BD平分∠ABC,CE平分∠DCF,∠ACE=90°(1)请问BD和CE是否平行?请你说明理由;
(2)AC和BD有何位置关系?请你说明判断的理由.
分析 (1)根据平行线性质得出∠ABC=∠DCF,根据角平分线定义求出∠2=∠4,根据平行线的判定推出即可;
(2)根据平行线性质得出∠DGC+∠ACE=180°,根据∠ACE=90°,求出∠DGC=90°,根据垂直定义推出即可.
解答  解:(1)BD∥CE.
解:(1)BD∥CE.
理由:∵AB∥CD,
∴∠ABC=∠DCF,
∴BD平分∠ABC,CE平分∠DCF,
∴∠2=$\frac{1}{2}$∠ABC,∠4=$\frac{1}{2}$∠DCF,
∴∠2=∠4,
∴BD∥CE(同位角相等,两直线平行);
(2)AC⊥BD,
理由:∵BD∥CE,
∴∠DGC+∠ACE=180°,
∴∠ACE=90°,
∴∠DGC=180°-90°=90°,
即AC⊥BD.
点评 本题考查了角平分线定义,平行线的性质和判定,垂直定义等知识点,解题时注意:①同位角相等,两直线平行;②两直线平行,同旁内角互补.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
16.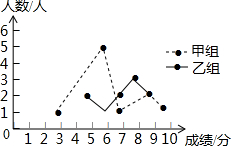 某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.
某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.
(1)求出下列成绩统计分析表中a,b的值:
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断,小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
 某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.
某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.(1)求出下列成绩统计分析表中a,b的值:
| 组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
| 甲组 | 6.8 | a | 3.76 | 90% | 30% |
| 乙组 | b | 7.5 | 1.96 | 80% | 20% |
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.
8.如果2是一元二次方程x2=c的一个根,则另一个根是( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
5.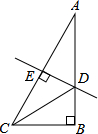 如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=3,则AB的长是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=3,则AB的长是( )
 如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=3,则AB的长是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=3,则AB的长是( )| A. | 9 | B. | 6$\sqrt{3}$ | C. | 6 | D. | 3$\sqrt{3}$ |
12.下列调查中,最适合采用普查方式的是( )
| A. | 对太湖流域水质情况的调查 | |
| B. | 对乘坐飞机的旅客是否携带违禁物品的调查 | |
| C. | 对一个城市每天丢弃塑料袋数量的调查 | |
| D. | 对无锡电视台某栏目收视率的调查 |

 如图,△ABC是等边三角形,BD是△ABC的角平分线,交边AC于点D,EC⊥BC于点C,CE=BD.求证:△ADE是等边三角形.
如图,△ABC是等边三角形,BD是△ABC的角平分线,交边AC于点D,EC⊥BC于点C,CE=BD.求证:△ADE是等边三角形.