题目内容
20.某学校组织学生去距离学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的3倍,设骑车学生的速度为x千米/小时,则可列方程为$\frac{10}{x}$-$\frac{10}{3x}$=$\frac{20}{60}$.分析 求速度,路程已知,根据时间来列等量关系.关键描述语为:“过了20分后,其余学生乘汽车出发,结果他们同时到达”;等量关系为:骑自行车同学所用时间-乘车同学所用时间=$\frac{20}{60}$小时.
解答 解:设骑车学生的速度为x千米/小时,根据题意,有:
$\frac{10}{x}$-$\frac{10}{3x}$=$\frac{20}{60}$.
故答案为:$\frac{10}{x}$-$\frac{10}{3x}$=$\frac{20}{60}$.
点评 本题考查由实际问题抽象出分式方程,分析题意,找到关键描述语,得到合适的等量关系是解决问题的关键.

练习册系列答案
相关题目
10.$\sqrt{(-3)^{2}}$的值等于( )
| A. | 3 | B. | -3 | C. | ±3 | D. | $\sqrt{3}$ |
11.某园林队计划由6名工人对200平方米的区域进行绿化,由于施工时增加了2名工人,结果比计划提前3小时完成任务,若每人每小时绿化面积相同,求每人每小时的绿化面积.设每人每小时的绿化面积为x平方米,列出满足题意的方程是( )
| A. | $\frac{200}{6x}$-$\frac{200}{(6+2)x}$=3 | B. | $\frac{200}{(6+2)x}$-$\frac{200}{6x}$=3 | C. | $\frac{200}{6x}$-$\frac{200}{2x}$=3 | D. | $\frac{200}{2x}$-$\frac{200}{6x}$=3 |
8.下列图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
15.方程x(x-3)+x-3=0的解是( )
| A. | 3 | B. | -3,1 | C. | -1 | D. | 3,-1 |
5. 如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为( )
如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为( )
 如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为( )
如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
9.在函数y=$\frac{{\sqrt{x+1}}}{x-2}$中,自变量x的取值范围是( )
| A. | x≤-1 | B. | x≥-1 | C. | x≤-1且x≠2 | D. | x≥-1且x≠2 |
10.一个质地均匀的正方体骰子的六个面上分别刻有“我”、“爱”、“爸”、“爸”、“妈”、“妈”六个字,如果将这个骰子掷一次,那么向上一面出现“妈”字的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
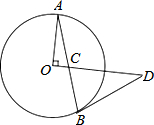 如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.
如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.