题目内容
12.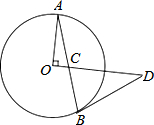 如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.
如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.(1)判断BD与圆O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.
分析 (1)连接OB,由BD=CD,利用等边对等角得到∠DCB=∠DBC,再由AO垂直于OD,得到三角形AOC为直角三角形,得到两锐角互余,等量代换得到OB垂直于BD,即可得证;
(2)设BD=x,则OD=x+1,在RT△OBD中,根据勾股定理得出32+x2=(x+1)2,通过解方程即可求得.
解答 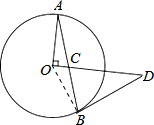 (1)证明:连接OB,
(1)证明:连接OB,
∵OA=OB,DC=DB,
∴∠A=∠ABO,∠DCB=∠DBC,
∵AO⊥OD,
∴∠AOC=90°,即∠A+∠ACO=90°,
∵∠ACO=∠DCB=∠DBC,
∴∠ABO+∠DBC=90°,即OB⊥BD,
则BD为圆O的切线;
(2)解:设BD=x,则OD=x+1,而OB=OA=3,
在RT△OBD中,OB2+BD2=OD2,
即32+x2=(x+1)2,
解得x=4,
∴线段BD的长是4.
点评 此题考查了切线的判定,勾股定理的应用,等腰三角形的性质,熟练掌握切线的判定方法是解本题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
2.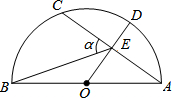 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于点D,连接BE.设∠BEC=α,则sinα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于点D,连接BE.设∠BEC=α,则sinα的值为( )
 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于点D,连接BE.设∠BEC=α,则sinα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于点D,连接BE.设∠BEC=α,则sinα的值为( )| A. | $\frac{3\sqrt{13}}{13}$ | B. | $\frac{2\sqrt{13}}{13}$ | C. | $\frac{\sqrt{13}}{13}$ | D. | $\frac{2}{3}$ |
3.某县为发展教育事业,加强了对教育经费的投入,2013年投入5000万元,预计2015年投入8000万元.设教育经费连续两年的年平均增长率为x,根据题意,下面所列方程正确的是( )
| A. | 5000(1+x)2=8000 | B. | 5000x2=8000 | ||
| C. | 5000(1+x%)2=8000 | D. | 5000(1+x)+5000(1+x)2=8000 |
7.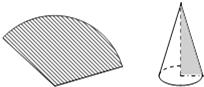 用圆心角为120°,半径6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )
用圆心角为120°,半径6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )
 用圆心角为120°,半径6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )
用圆心角为120°,半径6cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( )| A. | 2cm | B. | 3$\sqrt{2}$cm | C. | 4$\sqrt{2}$cm | D. | 4cm |
1.下列计算正确的是( )
| A. | 2-1=-2 | B. | (2x2)2=2x4 | C. | $\sqrt{25}=5$ | D. | (3.14-π)0=0 |
 如图,△ABC为⊙O的内接三角形,若AB为⊙O的直径,∠A=28°,则∠B=62度.
如图,△ABC为⊙O的内接三角形,若AB为⊙O的直径,∠A=28°,则∠B=62度.