题目内容
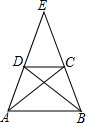如图，梯形ABCD中，AB∥DC，AC交BD于点F，延长AD、BC交于点E，DE=2，AD=3，求DF：BF的值．考点：相似三角形的判定与性质
专题：
分析：由AB∥DC，得到△EDC∽△EAB，△DFC∽△BFA，进而得到DF：BF=DE：AE，根据DE=2，AD=3，问题即可解决．
解答：
解：∵AB∥DC，
∴△EDC∽△EAB，△DFC∽△BFA，
∴DE：AE=DC：AB，DF：BF=DC：AB；
∴DF：BF=DE：AE，而DE=2，AD=3，
∴DF：BF=2：5．
解：∵AB∥DC，∴△EDC∽△EAB，△DFC∽△BFA，
∴DE：AE=DC：AB，DF：BF=DC：AB；
∴DF：BF=DE：AE，而DE=2，AD=3，
∴DF：BF=2：5．
点评：该题主要考查了相似三角形的判定及其性质的应用问题；解题的关键是深入观察图形，准确找出图形中的对应元素，正确判断出相似三角形，灵活利用相似三角形的性质来分析、判断、推理或解答．
练习册系列答案
相关题目
已知AB为⊙O的弦，C、D在AB上，且AC=CD=DB，求证：∠AOC=∠DOB．
如图，BM、CM平分△ABC的外角∠CBE和∠BCF，且BM与CM交于点M，ME⊥BE于E，MF⊥CF于点F．求证：ME=MF．
如图，已知∠1+∠2=180°，∠C=∠D，则∠A=∠F吗？为什么？