题目内容
两个相似多边形的面积之和为260cm2,相似比
,求较大多边形的面积.
| 2 |
| 3 |
考点:相似多边形的性质
专题:
分析:设较大多边形的面积为Scm2,则较小多边形的面积为(260-S)cm2,再根据相似比
即可得出S的值.
| 2 |
| 3 |
解答:解:∵两个相似多边形的面积之和为260cm2,
∴设较大多边形的面积为Scm2,则较小多边形的面积为(260-S)cm2.
∵相似比
,
∴
=(
)2,
解得S=180.
答:较大多边形的面积为180cm2.
∴设较大多边形的面积为Scm2,则较小多边形的面积为(260-S)cm2.
∵相似比
| 2 |
| 3 |
∴
| 260-S |
| S |
| 2 |
| 3 |
解得S=180.
答:较大多边形的面积为180cm2.
点评:本题考查的是相似多边形的性质,熟知相似多边形面积的比等于相似比的平方是解答此题的关键.

练习册系列答案
相关题目
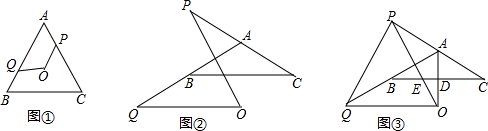
 如图,在△ABC中,sinA=
如图,在△ABC中,sinA=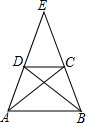 如图,梯形ABCD中,AB∥DC,AC交BD于点F,延长AD、BC交于点E,DE=2,AD=3,求DF:BF的值.
如图,梯形ABCD中,AB∥DC,AC交BD于点F,延长AD、BC交于点E,DE=2,AD=3,求DF:BF的值.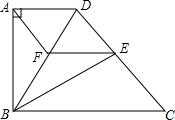 如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,若沿对角线BD翻折梯形ABCD,点A将恰好落在腰CD上的点E处.
如图,在直角梯形ABCD中,AD∥BC,AB⊥AD,若沿对角线BD翻折梯形ABCD,点A将恰好落在腰CD上的点E处.