题目内容
如图1,点A是线段BC上一点,△ABD和△ACE都是等边三角形.
(1)连接BE,CD,求证:BE=CD;
(2)如图2,作DP∥BC交EA于D′,交EC于P.
①判断△ADD′的形状,并证明;
②若△BDD′≌△D′PC,求证:AC=2AD′.
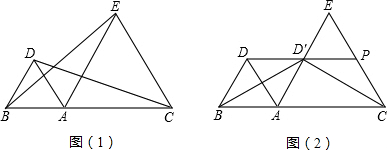
(1)连接BE,CD,求证:BE=CD;
(2)如图2,作DP∥BC交EA于D′,交EC于P.
①判断△ADD′的形状,并证明;
②若△BDD′≌△D′PC,求证:AC=2AD′.

考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)易证∠DAE=60°,可得∠DAC=∠BAE=120°,即可证明△DAC≌△BAE,可得BE=CD;
(2)①易证∠ADP=60°,根据∠DAE=60°即可判定△ADD′是等边三角形;
②易证BD=AD',根据△BDD′≌△D′PC,可得PD'=PC,即可求得∠ACD'=30°,根据30°角所对直角边是斜边一半即可解题.
(2)①易证∠ADP=60°,根据∠DAE=60°即可判定△ADD′是等边三角形;
②易证BD=AD',根据△BDD′≌△D′PC,可得PD'=PC,即可求得∠ACD'=30°,根据30°角所对直角边是斜边一半即可解题.
解答:证明:(1)∵△ABD和△ACE都是等边三角形,
∴AD=AB,AE=AC,∠BAD=∠EAC=60°,
∴∠DAE=60°,
∴∠DAC=∠BAE=120°,
∵在△DAC和△BAE中,
,
∴△DAC≌△BAE,(SAS)
∴BE=CD;
(2)①∵DP∥BC,
∴∠ADP=∠DAB=60°,
∵∠DAE=60°,
∴△ADD′是等边三角形;
②∵△ABD,△ADD′是等边三角形,
∴BD=AD,AD=AD',
∴BD=AD',
∵△BDD′≌△D′PC,
∴PD'=PC,
∵DP∥BC,
∴∠EPD=60°,
∴∠PCD'=30°,
∴∠ACD'=30°,
∵∠EAC=60°,
∴∠AD'C=90°,
∴AC=2AD'.
∴AD=AB,AE=AC,∠BAD=∠EAC=60°,
∴∠DAE=60°,
∴∠DAC=∠BAE=120°,
∵在△DAC和△BAE中,
|
∴△DAC≌△BAE,(SAS)
∴BE=CD;
(2)①∵DP∥BC,
∴∠ADP=∠DAB=60°,
∵∠DAE=60°,
∴△ADD′是等边三角形;
②∵△ABD,△ADD′是等边三角形,
∴BD=AD,AD=AD',
∴BD=AD',
∵△BDD′≌△D′PC,
∴PD'=PC,
∵DP∥BC,
∴∠EPD=60°,
∴∠PCD'=30°,
∴∠ACD'=30°,
∵∠EAC=60°,
∴∠AD'C=90°,
∴AC=2AD'.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了30°角所对直角边是斜边一半的性质,本题中求证△DAC≌△BAE是解题的关键.

练习册系列答案
相关题目
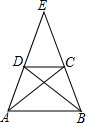 如图,梯形ABCD中,AB∥DC,AC交BD于点F,延长AD、BC交于点E,DE=2,AD=3,求DF:BF的值.
如图,梯形ABCD中,AB∥DC,AC交BD于点F,延长AD、BC交于点E,DE=2,AD=3,求DF:BF的值.