题目内容
18.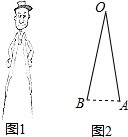 如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.
如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.(1)当∠AOB=20°时,求所作圆的半径;(结果精确到0.01cm)
(2)保持∠AOB=20°不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,求铅笔芯折断部分的长度.(结果精确到0.01cm)
(参考数据:sin10°≈0.174,cos10°≈0.985,sin20°≈0.342,cos20°≈0.940)
分析 (1)根据题意作辅助线OC⊥AB于点C,根据OA=OB=10cm,∠OCB=90°,∠AOB=18°,可以求得∠BOC的度数,从而可以求得AB的长;
(2)由题意可知,作出的圆与(1)中所作圆的大小相等,则AE=AB,然后作出相应的辅助线,画出图形,从而可以求得BE的长,本题得以解决.
解答  解:(1)作OC⊥AB于点C,如图2所示,
解:(1)作OC⊥AB于点C,如图2所示,
由题意可得,OA=OB=10cm,∠OCB=90°,∠AOB=20°,
∴∠BOC=10°
∴AB=2BC=2OB•sin10°≈2×10×0.174≈3.5cm,
即所作圆的半径约为3.5cm;
(2)作AD⊥OB于点D,作AE=AB,如图3所示,
∵保持∠AOB=20°不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,
∴折断的部分为BE,
∵∠AOB=20°,OA=OB,∠ODA=90°,
∴∠OAB=80°,∠OAD=70°,
∴∠BAD=10°,
∴BE=2BD=2AB•sin10°≈2×3.5×0.174≈1.2cm,
即铅笔芯折断部分的长度是1.2cm.
点评 本题考查解直角三角形的应用,解题的关键是明确题意,作出合适的辅助线,找出所求问题需要的条件.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
6.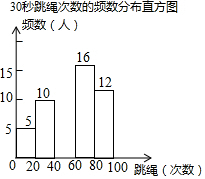 某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:
某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:
30秒跳绳次数的频数、频率分布表
根据以上图表信息,解答下列问题:
(1)表中的a=0.2,m=16;
(2)请把频数分布直方图补充完整;(画图后请标注相应的数据)
(3)若该校九年级共有600名学生,请你估计“30秒跳绳”的次数60次以上(含60次)的学生有多少人?
 某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:
某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:30秒跳绳次数的频数、频率分布表
| 成绩段 | 频数 | 频率 |
| 0≤x<20 | 5 | 0.1 |
| 20≤x<40 | 10 | a |
| 40≤x<60 | b | 0.14 |
| 60≤x<80 | m | c |
| 80≤x<100 | 12 | n |
(1)表中的a=0.2,m=16;
(2)请把频数分布直方图补充完整;(画图后请标注相应的数据)
(3)若该校九年级共有600名学生,请你估计“30秒跳绳”的次数60次以上(含60次)的学生有多少人?
13. 如何求tan75°的值?按下列方法作图可解决问题,如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BN上截取线段BD,使BD=AB,连接AD,依据此图可求得tan75°的值为( )
如何求tan75°的值?按下列方法作图可解决问题,如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BN上截取线段BD,使BD=AB,连接AD,依据此图可求得tan75°的值为( )
 如何求tan75°的值?按下列方法作图可解决问题,如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BN上截取线段BD,使BD=AB,连接AD,依据此图可求得tan75°的值为( )
如何求tan75°的值?按下列方法作图可解决问题,如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BN上截取线段BD,使BD=AB,连接AD,依据此图可求得tan75°的值为( )| A. | 2$-\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 1+$\sqrt{3}$ | D. | $\sqrt{3}-1$ |



 如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.