题目内容
13. 如何求tan75°的值?按下列方法作图可解决问题,如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BN上截取线段BD,使BD=AB,连接AD,依据此图可求得tan75°的值为( )
如何求tan75°的值?按下列方法作图可解决问题,如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BN上截取线段BD,使BD=AB,连接AD,依据此图可求得tan75°的值为( )| A. | 2$-\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 1+$\sqrt{3}$ | D. | $\sqrt{3}-1$ |
分析 在直角三角形ABC中,利用30度所对的直角边等于斜边的一半表示出AB的长,再利用勾股定理求出BC的长,由CB+BD求出CD的长,在直角三角形ACD中,利用锐角三角函数定义求出所求即可.
解答 解:在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,
∴AB=BD=2k,∠BAD=∠BDA=15°,BC=$\sqrt{3}$k,
∴∠CAD=∠CAB+∠BAD=75°,
在Rt△ACD中,CD=CB+BD=$\sqrt{3}$k+2k,
则tan75°=tan∠CAD=$\frac{CD}{AC}$=$\frac{\sqrt{3}k+2k}{k}$=2+$\sqrt{3}$,
故选B
点评 此题考查了解直角三角形,涉及的知识有:勾股定理,含30度直角三角形的性质,以及锐角三角函数定义,熟练掌握定理及性质是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 己知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是8$\sqrt{3}$.
己知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是8$\sqrt{3}$.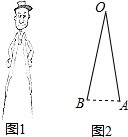 如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.
如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.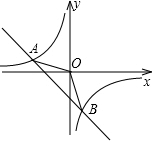 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.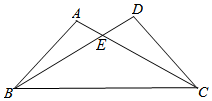 如图,已知∠A=∠D,有下列五个条件:①AE=DE,②BE=CE,③AB=DC,④∠ABC=∠DCB,⑤AC=BD,能证明△ABC与△DCB全等的条件有几个?并选择其中一个进行证明.
如图,已知∠A=∠D,有下列五个条件:①AE=DE,②BE=CE,③AB=DC,④∠ABC=∠DCB,⑤AC=BD,能证明△ABC与△DCB全等的条件有几个?并选择其中一个进行证明.