��Ŀ����
7��������ѧϰ������ѧ�̿����У���һ����ѧ����������������ǣ���һ�������۾���ֽƬABCD��ʹAD��BC�غϣ��õ��ۺ�EF����ֽƬչ������ͼ�٣���
�ڶ�������һ���۵�ֽƬ��ʹ��A����EF�ϣ���ʹ�ۺ۾�����B���õ��ۺ�BM��ͬʱ�õ��߶�BN����ͼ�ڣ���
��ͼ����ʾ����ƽ��ֱ������ϵ�������������⣺
������ֱ��BM�Ľ���ʽΪy=kx����k��ֵ��
������MN���ӳ��������ABCD�ı�BC���ڵ�P������εı�AB=a��BC=b��
��i����a=2��b=4����P������ꣻ
��ii����ֱ��д��a��bӦ�������������

���� ��������AN���ӳ�MN��BC�ڵ�P�����۵������ʿ�֤��BMPΪ�ȱ������Σ���M�����������k��ֵ��
����i����Rt��ABM�У��������ε����ʿ����BM�ij���������BP�ij��������P�����ꣻ
��ii���������֪BC��BP����Rt��BNP�У������Ǻ����Ķ������a��ʾ��BP����ɵõ�a��b�������������
��� �⣺
��������AN���ӳ�MN��BC�ڵ�P����ͼ��
��EF��ֱƽ��AB��
��AN=BN��
���۵�֪AB=BN��
��AN=AB=BN��
���ABNΪ�ȱ������Σ�
���ABN=60�㣬
���PBN=30�㣬
�ߡ�ABM=��NBM=30�㣬
���BNM=��A=90�㣬
���BPN=60�㣬��MBP=��MBN+��PBN=60�㣬
���BMP=60�㣬
���MBP=��BMP=��BPM=60�㣬
���BMP�ǵȱ������Σ�
�ߵ�M��ֱ��y=kx�ϣ�
��k=$\frac{{y}_{M}}{{x}_{M}}$=tan60��=$\sqrt{3}$��
����i���������֪AB=a=2��
��Rt��ABM��cos��ABM=$\frac{AB}{BM}$��
��$\frac{\sqrt{3}}{2}$=$\frac{2}{BM}$�����BM=$\frac{4\sqrt{3}}{3}$��
��BP=BM=$\frac{4\sqrt{3}}{3}$��
��P��$\frac{4\sqrt{3}}{3}$��0����
��ii���������֪BC��BP��
��Rt��BNP�У�BN=BA=a����PBN=30�㣬
��BP=$\frac{a}{cos30��}$��
��b��$\frac{a}{cos30��}$��
��a��$\frac{\sqrt{3}}{2}$b��
���� ����Ϊһ�κ������ۺ�Ӧ�ã��漰�۵������ʡ��ȱ������ε��ж������ʡ����Ǻ����Ķ����֪ʶ���ڣ�����֤�á�BMP�ǵȱ��������ǽ���Ĺؼ����ڣ��������BP��ֵ�ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�˯������ֶ��������
| ��� | ˯��ʱ��x��Сʱ�� |
| A | 4.5��x��5.5 |
| B | 5.5��x��6.5 |
| C | 6.5��x��7.5 |
| D | 7.5��x��8.5 |
| E | 8.5��x��9.5 |
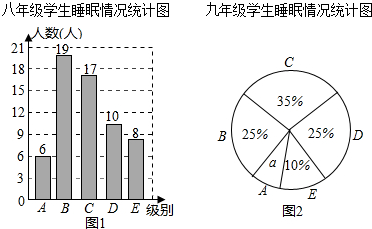
����ֱ��д��ͳ��ͼ��a��ֵ5%��
����˯��ʱ������6.5СʱΪ����˯�߲��㣬��Ӹ�У�ˡ����꼶�������һ��ѧ�������鵽������λѧ��˯�����ز���Ŀ����Էֱ��ж��
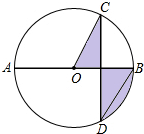 ��ͼ��AB�ǡ�O��ֱ������CD��AB����CDB=30�㣬CD=2$\sqrt{3}$������Ӱ����ͼ�ε����Ϊ��������
��ͼ��AB�ǡ�O��ֱ������CD��AB����CDB=30�㣬CD=2$\sqrt{3}$������Ӱ����ͼ�ε����Ϊ��������| A�� | 4�� | B�� | 2�� | C�� | �� | D�� | $\frac{2��}{3}$ |
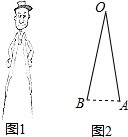 ��ͼ1��һ�����ͨԲ�棬ͼ2����ƽ��ʾ��ͼ��OA��֧�űۣ�OB����ת�ۣ�ʹ��ʱ���Ե�AΪ֧�ŵ㣬Ǧ��о�˵�B���Ƶ�A��ת����Բ����֪OA=OB=10cm��
��ͼ1��һ�����ͨԲ�棬ͼ2����ƽ��ʾ��ͼ��OA��֧�űۣ�OB����ת�ۣ�ʹ��ʱ���Ե�AΪ֧�ŵ㣬Ǧ��о�˵�B���Ƶ�A��ת����Բ����֪OA=OB=10cm��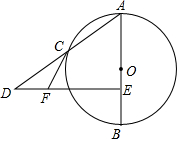 ��ͼ����֪AB�ǡ�O��ֱ������C�ڡ�O�ϣ���E��AB�ϣ���DE��AB��AC���ӳ����ڵ�D������C����O������CF��DE�ڵ�F��
��ͼ����֪AB�ǡ�O��ֱ������C�ڡ�O�ϣ���E��AB�ϣ���DE��AB��AC���ӳ����ڵ�D������C����O������CF��DE�ڵ�F��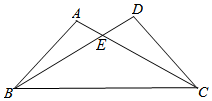 ��ͼ����֪��A=��D�������������������AE=DE����BE=CE����AB=DC���ܡ�ABC=��DCB����AC=BD����֤����ABC���DCBȫ�ȵ������м�������ѡ������һ������֤����
��ͼ����֪��A=��D�������������������AE=DE����BE=CE����AB=DC���ܡ�ABC=��DCB����AC=BD����֤����ABC���DCBȫ�ȵ������м�������ѡ������һ������֤���� ��ͼ���ڴ�¥AB����ǰ����һб��CD����֪б��CD��6$\sqrt{2}$�ף��½ǡ�DCE����45�㣬С����б���µĵ�C�����¥��B������Ϊ60�㣬��б���ϵĶ���D�����¥��B������Ϊ45�㣬���е�A��C��E��ͬһֱ���ϣ�
��ͼ���ڴ�¥AB����ǰ����һб��CD����֪б��CD��6$\sqrt{2}$�ף��½ǡ�DCE����45�㣬С����б���µĵ�C�����¥��B������Ϊ60�㣬��б���ϵĶ���D�����¥��B������Ϊ45�㣬���е�A��C��E��ͬһֱ���ϣ�