题目内容
8.我市某食品厂“端午节”期间,为了解市民对肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)四种不同口味粽子的喜爱情况,对某居民区进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将不完整的条形图补充完整.
(3)若居民区有6000人,请估计爱吃C粽的人数?

分析 (1)根据喜欢B粽的人数是60人,所占的比例是10%,据此即可求得调查的总人数;
(2)利用总人数减去其它组的人数即可求得喜欢C种粽子的人数,从而补全直方图;
(3)利用总人数6000乘以对应的百分比即可求得.
解答 解:(1)本次参加抽样调查的居民数是60÷10%=600(人);
(2)C组的人数是:600-180-60-240=120(人).
A类型百分比为$\frac{180}{600}$×100%=30%,
C类型百分比为$\frac{120}{600}$×100%=20%,
(3)估计爱吃C粽的人数是:6000×$\frac{120}{600}$=1200(人).
答:爱吃C粽的人数是1200人.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
18.已知:菱形的边长为4,且有一个内角为60°,一条直线将菱形ABCD分成面积相等的两个图形,设该直线与菱形的边交于点E,F,则线段EF的长m的取值范围( )
| A. | m=4或m=4$\sqrt{3}$ | B. | 4≤m≤4$\sqrt{3}$ | C. | 2$\sqrt{3}$≤m≤4$\sqrt{3}$ | D. | 2$\sqrt{3}$≤m≤4 |
20.已知关于x的方程x2+mx-6=0的一个根为2,则m的值及另一个根是( )
| A. | 1,3 | B. | -1,3 | C. | 1,-3 | D. | -1,-3 |
17.如果一个多边形的每一个内角都等于相邻外角的2倍,那么这个多边形的边数为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
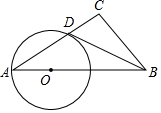 如图,Rt△ABC中∠C=90°,点O是AB边上一点,以OA为半径作⊙O,与边AC交于点D,连接BD,若∠DBC=∠A,求证:BD是⊙O的切线.
如图,Rt△ABC中∠C=90°,点O是AB边上一点,以OA为半径作⊙O,与边AC交于点D,连接BD,若∠DBC=∠A,求证:BD是⊙O的切线. 己知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是8$\sqrt{3}$.
己知菱形ABCD中,对角线AC与BD交于点O,∠BAD=120°,AC=4,则该菱形的面积是8$\sqrt{3}$. 在平行四边形ABCD中,点E是边AB的中点,AC、DE交于点F,则AF:FC=1:2.
在平行四边形ABCD中,点E是边AB的中点,AC、DE交于点F,则AF:FC=1:2.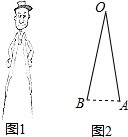 如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.
如图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,铅笔芯端点B可绕点A旋转作出圆.已知OA=OB=10cm.