题目内容
18.若0是关于x的一元二次方程(m-2)x2+3x+m2+2m-8=0的解,则求出m的值,并讨论方程根的情况.分析 将x=0代入原方程,可得出关于m的一元二次方程,解方程即可得出m的值,再根据原方程为一元二次方程,即二次项系数不为0,确定m的值,将m代入原方程,由根的判别式的符号即可得出根的情况.
解答 解:将x=0代入方程(m-2)x2+3x+m2+2m-8=0中,
得:m2+2m-8=0,
解得:m1=-4,m2=2.
∵原方程为一元二次方程,
∴m-2≠0,即m≠2.
∴m=-4.
当m=-4时,原方程为-6x2+3x=0,
∵△=32-4×(-6)×0=9>0,
∴原方程有两个不相等的实数根.
点评 本题考查了根的判别式以及一元二次方程的解,解题的关键是得出m的值.本题属于基础题,难度不大,解决该题型题目时,将x的值代入原方程求出方程系数中未知数的值是关键.

练习册系列答案
相关题目
9.下列图案中既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.tan30°的结果等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{1}{2}$ |
13. 如图所示,△ABC≌△DEC,则不能得到的结论是( )
如图所示,△ABC≌△DEC,则不能得到的结论是( )
 如图所示,△ABC≌△DEC,则不能得到的结论是( )
如图所示,△ABC≌△DEC,则不能得到的结论是( )| A. | AB=DE | B. | ∠A=∠D | C. | BC=CD | D. | ∠ACD=∠BCE |
3.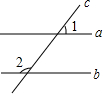 如图,平行线a,b被直线c所截,∠1=42°38′,则∠2的度数为( )
如图,平行线a,b被直线c所截,∠1=42°38′,则∠2的度数为( )
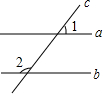 如图,平行线a,b被直线c所截,∠1=42°38′,则∠2的度数为( )
如图,平行线a,b被直线c所截,∠1=42°38′,则∠2的度数为( )| A. | 157°62′ | B. | 137°22′ | C. | 137°62′ | D. | 47°22′ |
10.若$\sqrt{a+b+5}$+|2a-b+1|=0,则(b-a)2016的值为( )
| A. | -1 | B. | 1 | C. | 52015 | D. | -52015 |
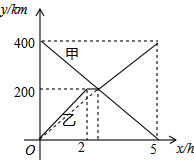 甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题:
甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题: 如图,已知△ABC中,AB=AC,将△ABC沿着EF折叠,使点B落在边AC上,记为点D,且DF=DC.
如图,已知△ABC中,AB=AC,将△ABC沿着EF折叠,使点B落在边AC上,记为点D,且DF=DC.