题目内容
15.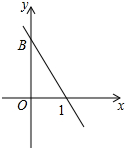 如图,在平面直角坐标系xOy中,直线$y=-\frac{3}{2}x+b$经过第一、二、四象限,与y轴交于点B,点A(2,m)在这条直线上,连结AO,△AOB的面积等于2.
如图,在平面直角坐标系xOy中,直线$y=-\frac{3}{2}x+b$经过第一、二、四象限,与y轴交于点B,点A(2,m)在这条直线上,连结AO,△AOB的面积等于2.(1)求b的值;
(2)如果反比例函数$y=\frac{k}{x}$(k是常量,k≠0)的图象经过点A,求这个反比例函数的解析式.
分析 (1)作AC⊥y轴,C为垂足,则AC是OB边上的高,根据A的坐标可知AC=2,由一次函数的解析式得出B(0,b),则OB=b,然后根据三角形的面积列出方程,解方程求得即可;
(2)把A(2,m)代入$y=-\frac{3}{2}x+2$求出m,得出A的坐标,代入$y=\frac{k}{x}$根据待定系数法即可求得.
解答 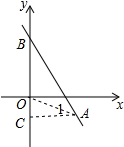 解:(1)∵直线$y=-\frac{3}{2}x+b$与y轴交于点B,
解:(1)∵直线$y=-\frac{3}{2}x+b$与y轴交于点B,
∴点B的坐标为(0,b).
作AC⊥y轴,C为垂足,则AC是OB边上的高,
∵点A的坐标为(2,m),
∴AC=2.
又∵△AOB的面积等于2,
∴$\frac{1}{2}b×2=2$,
∴b=2.
(2)∵点A(2,m)在直线$y=-\frac{3}{2}x+2$
∴$m=-\frac{3}{2}×2+2=-1$,
∴A的坐标为(2,-1).
又∵反比例函数$y=\frac{k}{x}$(k是常量,k≠0)的图象经过点A,
∴$-1=\frac{k}{2}$,即k=-2,
∴这个反比例函数的解析式为$y=-\frac{2}{x}$.
点评 本题主要考查了反比例函数与一次函数的交点问题,解题的关键是正确求出一次函数的解析式.

练习册系列答案
相关题目
10.已知不等式4x-a≤0的正整数解是1,2,则a的取值范围是( )
| A. | 8<a<12 | B. | 8≤a<12 | C. | 8<a≤12 | D. | 8≤a≤12 |
 如图,AB∥CD,EF分别交AB,CD于点E,F,∠1=63°,则∠2=117°.
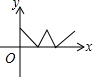
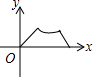
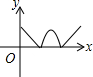
如图,AB∥CD,EF分别交AB,CD于点E,F,∠1=63°,则∠2=117°. 如图,在等边三角形ABC中,AB=2,动点P从点A出发,沿三角形边界按顺时针方向匀速运动一周,点Q在线段AB上,且满足AQ+AP=2.设点P运动的时间为x,AQ的长为y,则y与x的函数图象大致是( )
如图,在等边三角形ABC中,AB=2,动点P从点A出发,沿三角形边界按顺时针方向匀速运动一周,点Q在线段AB上,且满足AQ+AP=2.设点P运动的时间为x,AQ的长为y,则y与x的函数图象大致是( )