题目内容
11．解不等式组：$\left\{\begin{array}{l}{4（x-1）＜3x-4（1）}\\{\frac{1+2x}{3}＞x-1（2）}\end{array}\right.$请结合题意填空：完成本题的解答：
（Ⅰ）解不等式（1），得x＜0；
（Ⅱ）解不等式（2），得x＜4；
（Ⅲ）把不等式（1）和（2）的解集在数轴上表示出来：
（Ⅳ）原不等式组的解集为x＜0．
分析 分别求出每一个不等式的解集，根据不等式在数轴上的表示，由公共部分呢即可确定不等式组的解集．
解答 解：（Ⅰ）解不等式（1），得x＜0；
（Ⅱ）解不等式（2），得x＜4；
（Ⅲ）把不等式（1）和（2）的解集在数轴上表示出来：
（Ⅳ）原不等式组的解集为：x＜0，
故答案为：x＜0，x＜4，x＜0．
点评 本题考查的是解一元一次不等式组，正确求出每一个不等式解集是解答此题的关键．
练习册系列答案
相关题目
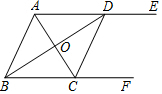如图，AE∥BF，AC平分∠BAE，且交BF于点C，BD平分∠ABF，且交AE于点D，连接CD．
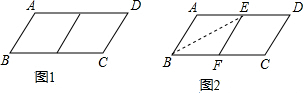邻边不相等的平行四边形纸片，减去一个菱形，余下一个四边形，称为第一次操作，在余下的四边形纸片中再剪去一个菱形，余下一个四边形，称为第二次操作，…依此类推，若第n次余下的四边形是菱形，则称原平行四边形为n阶准菱形，如图1，平行四边形ABCD中，若AB=1，BC=2，则平行四边形ABCD为1阶准菱形．
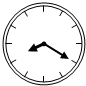小明在他家里的时钟上安装了一个电脑软件，他设定当钟声在n点钟响起后，下一次则在（3n-1）小时后响起，例如钟声第一次在3点钟响起，那么第2次在（3×3-1=8）小时后，也就是11点响起，第3次在（3×11-1=32）小时后，即7点响起，以此类推…；现在第1次钟声响起时为2点钟，那么第3次响起时为3点，第2017次响起时为11点（如图钟表，时间为12小时制）．
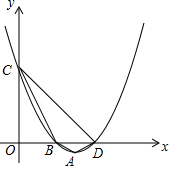已知二次函数y=x2-（a-1）x+a-2，其中a是常数．
解不等式组$\left\{\begin{array}{l}{2（x+1）≥0，①}\\{1-\frac{x}{3}＞\frac{x-3}{6}，②}\end{array}\right.$并把解集在数轴上表示出来．