题目内容
8.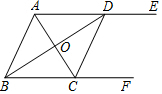 如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.
如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.(1)求证:四边形ABCD是菱形;
(2)若∠ADB=30°,BD=6,求AD的长.
分析 (1)由平行线的性质和角平分线定义得出∠ABD=∠ADB,证出AB=AD,同理:AB=BC,得出AD=BC,证出四边形ABCD是平行四边形,即可得出结论;
(2)由菱形的性质得出AC⊥BD,OD=OB=$\frac{1}{2}$BD=3,再由三角函数即可得出AD的长.
解答 (1)证明:∵AE∥BF,
∴∠ADB=∠CBD,
又∵BD平分∠ABF,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
同理:AB=BC,
∴AD=BC,
∴四边形ABCD是平行四边形,
又∵AB=AD,
∴四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,BD=6,
∴AC⊥BD,OD=OB=$\frac{1}{2}$BD=3,
∵∠ADB=30°,
∴cos∠ADB=$\frac{OD}{AD}$=$\frac{\sqrt{3}}{2}$,
∴AD=$\frac{3}{\frac{\sqrt{3}}{2}}$=2$\sqrt{3}$.
点评 本题考查了菱形的判定与性质、平行线的性质、等腰三角形的判定、平行四边形的判定、三角函数等知识;熟练掌握菱形的判定与性质是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.下列各式由左到右的变形中,属于分解因式的是( )
| A. | a(m+n)=am+an | B. | a2-b2-c2=(a-b)(a+b)-c2 | ||
| C. | 10x2-5x=5x(2x-1) | D. | x2-16+6x=(x+4)(x-4)+6x |
19. 如图为张小亮的答卷,他的得分应是( )
如图为张小亮的答卷,他的得分应是( )
 如图为张小亮的答卷,他的得分应是( )
如图为张小亮的答卷,他的得分应是( )| A. | 100分 | B. | 80分 | C. | 60分 | D. | 40分 |
20. 如图所示的圆锥的主视图是( )
如图所示的圆锥的主视图是( )
 如图所示的圆锥的主视图是( )
如图所示的圆锥的主视图是( )| A. |  | B. |  | C. |  | D. |  |
17.如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )


| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
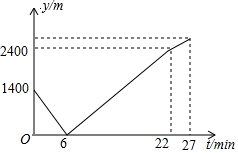 小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法: 如图所示的几何体是由6个大小完全一样的正方体组合而成的,它的俯视图是( )
如图所示的几何体是由6个大小完全一样的正方体组合而成的,它的俯视图是( )



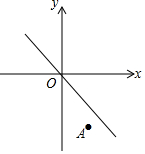 如图,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为($\frac{2}{3}$,0).
如图,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为($\frac{2}{3}$,0).