题目内容
14.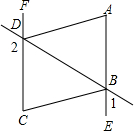 如图,∠1+∠2=180°,DA平分∠BDF,BC平分∠DBE,求证:AD∥BC.
如图,∠1+∠2=180°,DA平分∠BDF,BC平分∠DBE,求证:AD∥BC.
分析 首先证明∠FDB=∠DBE,再利用角平分线的性质可得∠ADB=∠DBC,然后根据内错角相等,两直线平行可得结论.
解答 证明:∵∠2=∠FDB,∠1+∠2=180°,
∴∠FDB+∠1=180°,
∵∠DBE+∠1=180°,
∴∠FDB=∠DBE,
∵DA平分∠BDF,BC平分∠DBE,
∴∠ADB=$\frac{1}{2}$∠FDB,∠DBC=$\frac{1}{2}$∠DBE,
∴∠ADB=∠DBC,
∴AD∥CB.
点评 此题主要考查了平行线的判定,关键是掌握内错角相等,两直线平行.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.下列说法中不正确的是( )
| A. | -$\sqrt{5}$是5的平方根 | B. | -3是-27的立方根 | ||
| C. | 4的平方根是16 | D. | (-2)2的算术平方根是2 |
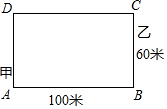 如图,有一条长方形跑道,甲从A点出发,乙从C点发.同时按逆时针方奔跑.甲速每秒6.25米,乙速每秒5米.跑道长100米,宽60米.当甲、乙每次跑道拐点A、B、C、D时都要停留5秒.问当甲第1次追上乙时,甲、乙各跑了多少米.
如图,有一条长方形跑道,甲从A点出发,乙从C点发.同时按逆时针方奔跑.甲速每秒6.25米,乙速每秒5米.跑道长100米,宽60米.当甲、乙每次跑道拐点A、B、C、D时都要停留5秒.问当甲第1次追上乙时,甲、乙各跑了多少米. 已知△ABC,如图,过点A画△ABC的角平分线AD、中线AE和高线AF.
已知△ABC,如图,过点A画△ABC的角平分线AD、中线AE和高线AF.