题目内容
2.用配方法解方程:(1)4x2+8x+1=0
(2)y2+3y-7=0
(3)2x2-7x+6=0
(4)x2+2mx-n2=0.
分析 (1)先把方程化为x2+2x=-$\frac{1}{4}$,然后利用配方法解方程;
(2)先把方程化为y2+3y=7,然后利用配方法解方程;
(3)先把方程化为x2-$\frac{7}{2}$x=-3,然后利用配方法解方程;
(4)先把方程化为x2+2mx=n2,然后利用配方法解方程.
解答 解:(1)x2+2x=-$\frac{1}{4}$,
x2+2x+1=-$\frac{1}{4}$+1,
(x+1)2=$\frac{3}{4}$,
x+1=±$\frac{\sqrt{3}}{2}$,
所以x1=-1+$\frac{\sqrt{3}}{2}$,x2=-1-$\frac{\sqrt{3}}{2}$;
(2)y2+3y=7,
y2+3y+($\frac{3}{2}$)2=7+($\frac{3}{2}$)2,
(y+$\frac{3}{2}$)2=$\frac{37}{4}$,
y+$\frac{3}{2}$=±$\frac{\sqrt{37}}{2}$,
所以y1=$\frac{-3+\sqrt{37}}{2}$,y2=$\frac{-3-\sqrt{37}}{2}$;
(3)x2-$\frac{7}{2}$x=-3,
x2-$\frac{7}{2}$x+($\frac{7}{4}$)2=-3+($\frac{7}{4}$)2,
(x-$\frac{7}{4}$)2=$\frac{1}{16}$,
x-$\frac{7}{4}$=±$\frac{1}{4}$,
所以x1=2,x2=$\frac{3}{2}$;
(4)x2+2mx=n2,
x2+2mx+m2=m2+n2,
(x+m)2=m2+n2,
x+m=±$\sqrt{{m}^{2}+{n}^{2}}$,
所以x1=-m+$\sqrt{{m}^{2}+{n}^{2}}$,x2=-m-$\sqrt{{m}^{2}+{n}^{2}}$.
点评 本题考查了解一元二次方程-配方法:将一元二次方程配成(x+m)2=n的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法.

 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案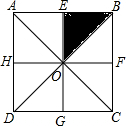 如图,正方形ABCD的所有对称轴交于点O,并把正方形分割成8个小的直角等腰三角形,△BEO为其中之一,通过不同的变换可使得△BEO分别与另外的7个小三角形重合.若通过轴对称变换,△BEO可与另外的4个三角形重合;若通过平移,△BEO可与另外的1个三角形重合.
如图,正方形ABCD的所有对称轴交于点O,并把正方形分割成8个小的直角等腰三角形,△BEO为其中之一,通过不同的变换可使得△BEO分别与另外的7个小三角形重合.若通过轴对称变换,△BEO可与另外的4个三角形重合;若通过平移,△BEO可与另外的1个三角形重合. 如图,在长方体ABCD-EFGH中,与棱HD异面的棱是EF、AB、GF、BC.
如图,在长方体ABCD-EFGH中,与棱HD异面的棱是EF、AB、GF、BC.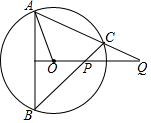 如图,AB为圆O的弦,QO⊥AB,QA交⊙O于C,BC交QO于P,求证:OA2=OP•OQ.
如图,AB为圆O的弦,QO⊥AB,QA交⊙O于C,BC交QO于P,求证:OA2=OP•OQ.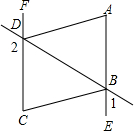 如图,∠1+∠2=180°,DA平分∠BDF,BC平分∠DBE,求证:AD∥BC.
如图,∠1+∠2=180°,DA平分∠BDF,BC平分∠DBE,求证:AD∥BC. 如图,已知CD⊥AB,BE⊥AC,证明:$\frac{AB}{AE}$=$\frac{AC}{AD}$.
如图,已知CD⊥AB,BE⊥AC,证明:$\frac{AB}{AE}$=$\frac{AC}{AD}$.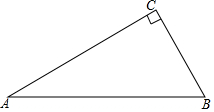 如图,△ABC中,∠C=90°,∠A=30°.
如图,△ABC中,∠C=90°,∠A=30°.