题目内容
10.(1)先化简,再求值:(2-$\frac{x+6}{x+2}$)÷$\frac{x-2}{{x}^{2}-4}$,其中x=2+$\sqrt{2}$;(2)解不等式:$\frac{x-1}{2}$-$\frac{2x+1}{3}$≥-1.
分析 (1)先根据分式混合运算的法则把原式进行化简,再求出x的值,代入进行计算即可;
(2)利用不等式的基本性质,即可得到结论.
解答 解:(1)(2-$\frac{x+6}{x+2}$)÷$\frac{x-2}{{x}^{2}-4}$=$\frac{x-2}{x+2}$•$\frac{(x+2)(x-2)}{x-2}$=x-2,
当x=2+$\sqrt{2}$时,原式=$\sqrt{2}$;
(2)$\frac{x-1}{2}$-$\frac{2x+1}{3}$≥-1,
3(x-1)-2(2x-1)≥-6,
3x-3-4x+2≥-6,
∴x≤5.
点评 此题主要考查了分式的化简求值问题,要熟练掌握,先把分式化简后,再把分式中未知数对应的值代入求出分式的值.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
1. 如图,AB是⊙O直径,C,D是圆上的点,若∠D=20°,则∠BAC的值是( )
如图,AB是⊙O直径,C,D是圆上的点,若∠D=20°,则∠BAC的值是( )
 如图,AB是⊙O直径,C,D是圆上的点,若∠D=20°,则∠BAC的值是( )
如图,AB是⊙O直径,C,D是圆上的点,若∠D=20°,则∠BAC的值是( )| A. | 20° | B. | 60° | C. | 70° | D. | 80° |
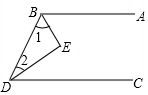 (1)已知a=(-2)3,b=-$\frac{\sqrt{5}}{2}$+$\sqrt{\frac{9}{4}}$,c=${(\sqrt{\frac{17}{2}})}^{2}$,d=|2-$\sqrt{5}$|.
(1)已知a=(-2)3,b=-$\frac{\sqrt{5}}{2}$+$\sqrt{\frac{9}{4}}$,c=${(\sqrt{\frac{17}{2}})}^{2}$,d=|2-$\sqrt{5}$|.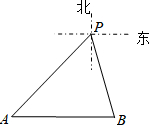 如图,某天上午,一渔船在我海上指挥中心P的南偏东15°方向的B处遇险,在海上指挥中心P的南偏西45°方向A处的海口舰接到求救信号后立刻前往救援,此时,海口舰与指挥中心P相距10($\sqrt{3}$+1)海里,渔船B在海口舰A的正东方向.求此时渔船B与海口舰A的距离(结果保留根号).
如图,某天上午,一渔船在我海上指挥中心P的南偏东15°方向的B处遇险,在海上指挥中心P的南偏西45°方向A处的海口舰接到求救信号后立刻前往救援,此时,海口舰与指挥中心P相距10($\sqrt{3}$+1)海里,渔船B在海口舰A的正东方向.求此时渔船B与海口舰A的距离(结果保留根号).