题目内容
15.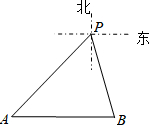 如图,某天上午,一渔船在我海上指挥中心P的南偏东15°方向的B处遇险,在海上指挥中心P的南偏西45°方向A处的海口舰接到求救信号后立刻前往救援,此时,海口舰与指挥中心P相距10($\sqrt{3}$+1)海里,渔船B在海口舰A的正东方向.求此时渔船B与海口舰A的距离(结果保留根号).
如图,某天上午,一渔船在我海上指挥中心P的南偏东15°方向的B处遇险,在海上指挥中心P的南偏西45°方向A处的海口舰接到求救信号后立刻前往救援,此时,海口舰与指挥中心P相距10($\sqrt{3}$+1)海里,渔船B在海口舰A的正东方向.求此时渔船B与海口舰A的距离(结果保留根号).
分析 过B作BC⊥AP于C,设PC=x,则BC=$\sqrt{3}$x,AC=$\sqrt{3}$x,AB=$\sqrt{6}$x,在Rt△ABC中,根据勾股定理可得PC的长,进一步得到渔船B与海口舰A的距离.
解答 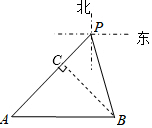 解:过B作BC⊥AP于C,
解:过B作BC⊥AP于C,
由题意知:∠ABC=45°,∠PBC=30°,
设PC=x,
在Rt△PBC中,∠PBC=30°,
则BC=$\sqrt{3}$x,
在Rt△ABC中,∠ABC=45°,
则AC=$\sqrt{3}$x,AB=$\sqrt{6}$x,
∴$\sqrt{3}$x+x=$10({\sqrt{3}+1})$.
解得x=10,
∴AB=10$\sqrt{6}$(海里).
答:B与海口舰A的距离为10$\sqrt{6}$海里.
点评 本题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将勾股定理的应用的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
5.若$\sqrt{(m-2)^{2}}$+|m-3|化简的结果为一个常数,则m的取值范围是( )
| A. | m>0 | B. | m≥3 | C. | m≤2 | D. | 2≤m≤3 |
6.下列数没有算术平方根是( )
| A. | 5 | B. | 6 | C. | 0 | D. | -3 |
3.下列图形是轴对称图形但不是中心对称图形的是( )
| A. | 线段 | B. | 等边三角形 | C. | 正方形 | D. | 圆 |
7.已知扇形的圆心角为150°,半径为6cm,则该扇形的侧面积为( )
| A. | 5πcm2 | B. | 15πcm2 | C. | 20πcm2 | D. | 30πcm2 |
5.在下列几个几何体中,主视图与俯视图都是圆的是( )
| A. |  | B. |  | C. |  | D. |  |