化简:-2(2a2-ab), (2)(x-1+$\frac{1-x}{x+1}$)÷$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$．题目和参考答案——青夏教育精英家教网—

题目内容

19．化简：
（1）（-2a-b）（-2a+b）-2（2a²-ab）；
（2）（x-1+$\frac{1-x}{x+1}$）÷$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$．

分析（1）根据整式的运算法则即可求出答案．
（2）根据分式的运算法则即可求出答案．

解答解：（1）原式=（-2a-b）（-2a+b）-2（2a²-ab）
=2ab-b²
（2）原式=$\frac{（x-1）（x+1）+1-x}{x+1}•\frac{（x+1）（x-1）}{{{{（x-1）}^2}}}$
=$\frac{{{x^2}-1+1-x}}{x-1}$
=x

点评本题考查学生的运算能力，解题的关键是熟练运用运算法则，本题属于基础题型．

练习册系列答案

相关题目

9．

在等腰Rt△ABC中，AB=AC，∠DAE=45°，若BC=10，求BE•CD．

10．（1）先化简，再求值：（2-$\frac{x+6}{x+2}$）÷$\frac{x-2}{{x}^{2}-4}$，其中x=2+$\sqrt{2}$；
（2）解不等式：$\frac{x-1}{2}$-$\frac{2x+1}{3}$≥-1．

7．已知扇形的圆心角为150°，半径为6cm，则该扇形的侧面积为（　　）

14．

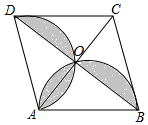如图，菱形ABCD的对角线AC，BD相交于点O，AC=6，BD=8，分别以AB、AD为直径作一个半圆，则图中阴影部分的面积为（　　）

4．正五边形ABCDE．
（1）若M，N分别是边DE，AE的中点，连接CM，DN，求证：$\frac{1}{2}$DE²=DP•DN：
（2）若O为边BD的中点，连接EO并延长交BC于点G．求$\frac{BG}{CG}$的值；
（3）若G为BC的中点．连接EG交BD于H．若AB=$\sqrt{5}$+1．直接写出BH的长

11．定义新运算：对于任意实数a，b（其中a≠0），都有a?b=$\frac{1}{a}$-$\frac{a-b}{a}$，等式右边是通常的加法、减法及除法运算，例如2?3=$\frac{1}{2}$-$\frac{2-3}{2}$=$\frac{1}{2}$+$\frac{1}{2}$=1．
（1）求（-2）?3的值；
（2）若x?2=1，求x的值．

8．已知点P（a+1，-$\frac{a}{2}$+1）关于y轴的对称点在第一象限，则a的范围在数轴上表示正确的是（　　）

9．

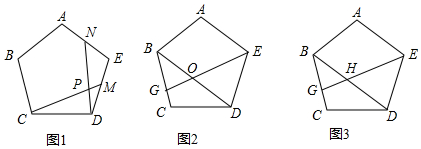
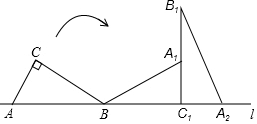如图，Rt△ABC的斜边AB在直线l上，AC=1，AB=2．将Rt△ABC绕点B在平面内按顺时针方向旋转，使边BC落在直线l上，得到△A₁BC₁，再将△A₁BC₁绕点C₁在平面内按顺时针方向旋转，使边A₁C₁落到直线l上，得到△A₂B₁C₁，则点A所经过的两条弧的长度和为$\frac{13}{6}$π．

试题分类