题目内容
（1）计算：（sin30°）-2+（
）0-|3-
|+83×（-0.125）3．
（2）先化简再求值：
+
，其中
+36a2+b2-12ab=0．
| 3 | ||
5-
|
| 18 |
（2）先化简再求值：
| ab+a |
| b2-1 |
| b-1 |
| b2-2b+1 |
| b-2 |
考点：分式的化简求值,非负数的性质：算术平方根,零指数幂,负整数指数幂,二次根式的混合运算,配方法的应用
专题：
分析：（1）先计算负整数指数幂、零指数幂、绝对值；然后根据实数混合运算法则进行解答；
（2）先约分化简，然后代入求值．
（2）先约分化简，然后代入求值．
解答：解：（1）原式=（
）-2+1+3-
+83×（-
）3．
=4+4-3
-1
=7-3
；
（2）由
+36a2+b2-12ab=0，得
+（6a-b）2=0．
则b-2=0，6a-b=0，
解得 b=2，a=
．
+
=
+
=
+
=
=
=
．
| 1 |
| 2 |
| 18 |
| 1 |
| 8 |
=4+4-3
| 2 |
=7-3
| 2 |
（2）由
| b-2 |
| b-2 |
则b-2=0，6a-b=0，
解得 b=2，a=
| 1 |
| 3 |
| ab+a |
| b2-1 |
| b-1 |
| b2-2b+1 |
=
| a(b+1) |
| (b+1)(b-1) |
| b-1 |
| (b-1)2 |
=
| a |
| b-1 |
| 1 |
| b-1 |
=
| a+1 |
| b-1 |
=
| ||
| 2-1 |
=
| 4 |
| 3 |
点评：本题综合考查了二次根式的混合运算，配方法的应用，零指数幂和负整数指数幂等知识点．解答此题的关键是把分式化到最简，然后代值计算．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知三点P1（x1，y1），P2（x2，y2），P3（x3，y3）都在反比例函数y=-
的图象上，且x1＜0＜x2＜x3，则下列式子正确的是（ ）
| 2 |
| x |
| A、y1＞y2＞y3 |
| B、y1＞y3＞y2 |
| C、y2＞y3＞y1 |
| D、y3＞y2＞y1 |
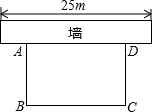如图所示：某居民小区要在一块要边靠墙（墙长25m）的空地上修建一个矩形花园ABCD，花园的一边靠墙，另三边由总长为40m的栅栏围成．
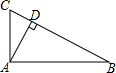如图所示，AD⊥BC，垂足为D，如果CD=1，AD=2，BD=4，那么∠BAC是直角吗？请说明理由．
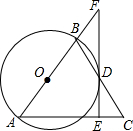如图在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC于E交AB的延长线于点F，