题目内容
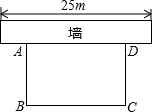 如图所示:某居民小区要在一块要边靠墙(墙长25m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边由总长为40m的栅栏围成.
如图所示:某居民小区要在一块要边靠墙(墙长25m)的空地上修建一个矩形花园ABCD,花园的一边靠墙,另三边由总长为40m的栅栏围成.①若要求花园面积为182m2,请你给出设计方案.
②花园的面积250m2吗?若能,请你给出方案;若不能,说明理由.
考点:一元二次方程的应用
专题:几何图形问题
分析:(1)本题可设出花园的一边,然后根据矩形的面积=长×宽,用未知数表示出花园的面积,要求花园的面积能否达到182平方米,只需让花园的面积先等于182,然后看得出的方程有没有解,如果有就证明可以达到182平方米,如果方程无解,说明不能达到182平方米;
(2)本题方法与(1)一样.
(2)本题方法与(1)一样.
解答:解:(1)设BC长为xm(0<x≤25),则AB的长为
m,依题意,得:
•x=182,
解得x1=14,x2=26(不合题意舍去),
=
=13,
则AB的长为13m,BC的长为14m.
故我的设计方案是长14米,宽13米.
(2)设BC长为xm(0<x≤25),则AB的长为
m,依题意,得:
•x=250,
化简得x2-40x+500=0,
△=(-40)2-4×500=-400<0,
故方程无解,
故不能使得花园的面积250m2.
| 40-x |
| 2 |
| 40-x |
| 2 |
解得x1=14,x2=26(不合题意舍去),
| 40-x |
| 2 |
| 40-14 |
| 2 |
则AB的长为13m,BC的长为14m.
故我的设计方案是长14米,宽13米.
(2)设BC长为xm(0<x≤25),则AB的长为
| 40-x |
| 2 |
| 40-x |
| 2 |
化简得x2-40x+500=0,
△=(-40)2-4×500=-400<0,
故方程无解,
故不能使得花园的面积250m2.
点评:本题考查了一元二次方程的运用,是一道数形结合试题.要读清题意,熟记一元二次方程根与系数的关系.读懂题意,找到等量关系准确的列出方程是解题的关键.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
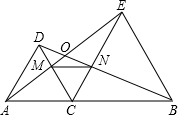 如图△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:
如图△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论: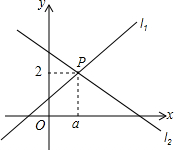 如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2).
如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2).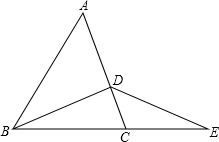 如图:D为AC上一点,E为BC延长线上一点,连接BD,DE.
如图:D为AC上一点,E为BC延长线上一点,连接BD,DE.