题目内容
已知y=
+
,求y的最小值.
| x2-2x+2 |
| x2+2x+2 |
考点:无理函数的最值
专题:
分析:整理式子,可以把y看作平面直角坐标系中点P(x,0)到点A(1,1)的距离和点P(x,0)到点B(-1,-1)的距离之和,然后得出当A、P、B三点共线时,点P在AB之间时y值最小,求出最小值即可.
解答:解:∵y=
+
=
+
,
设P(x,0),A(1,1),B(-1,-1),
∴
可看作为在平面直角坐标系中点P(x,0)到点A(1,1)的距离,
可看作为在平面直角坐标系中点P(x,0)到点B(-1,-1)的距离,
当A、P、B三点共线时,点P在AB之间时y值最小,
∴此时y最小=|AB|=
=2
.
| (x-1)2+12 |
| (x+1)2+12 |
=
| (x-1)2+(0-1)2 |
| (x+1)2+(0+1)2 |
设P(x,0),A(1,1),B(-1,-1),
∴
| (x-1)2+(0-1)2 |
| (x+1)2+(0+1)2 |
当A、P、B三点共线时,点P在AB之间时y值最小,
∴此时y最小=|AB|=
| (1+1)2+(1+1)2 |
| 2 |
点评:本题考查了无理函数的最值问题,解答本题的关键是把y看作平面直角坐标系中点P(x,0)到点A(1,1)的距离和点P(x,0)到点B(-1,-1)的距离之和,难度较大.

练习册系列答案
相关题目
下列各对单项式是同类项的是( )
| A、-x3y2与3x3y2 |
| B、-x与y |
| C、3与3a |
| D、3ab2与a2b |
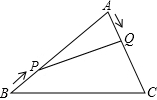 如图,在△ABC中,∠A=60°,AB=18,AC=12,点P从点B出发,以3cm/s的速度向点A运动,点Q从点A同时出发以2cm/s的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动.
如图,在△ABC中,∠A=60°,AB=18,AC=12,点P从点B出发,以3cm/s的速度向点A运动,点Q从点A同时出发以2cm/s的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动.