题目内容
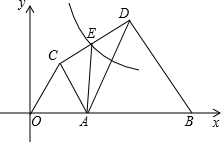 如图,点B的坐标为(10,0),点A是OB上的一个动点,且OA<AB,分别以OA、AB为边在x轴上方作等边三角形OAC和等边三角形ABD,连接CD,E为CD的中点,双曲线y=
如图,点B的坐标为(10,0),点A是OB上的一个动点,且OA<AB,分别以OA、AB为边在x轴上方作等边三角形OAC和等边三角形ABD,连接CD,E为CD的中点,双曲线y=| k |
| x |
| ||
| 2 |
考点:反比例函数综合题
专题:代数几何综合题,待定系数法
分析:作EH⊥OB于H点,则EH为梯形CMND的中位线,根据梯形中位线的性质得EH=
(CM+DN)=
,HM=
MN=
(ON-OM)=
,得到AH=
-
t或
t-
,
再利用勾股定理得AE2=AH2+EH2,即(
)2+(
)2=(
)2,解得t1=3,t2=7,然后分别确定E点坐标,再代入反比例函数解析式可得到k的值.,
| 1 |
| 2 |
5
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
再利用勾股定理得AE2=AH2+EH2,即(
5
| ||
| 2 |
| 5-t |
| 2 |
| ||
| 2 |
解答: 解:作EH⊥OB于H点,如图,
解:作EH⊥OB于H点,如图,
∵E为CD的中点,
∴EH为梯形CMND的中位线,
∴EH=
(CM+DN)=
[
t+
(10-t)]=
,HM=
MN=
(ON-OM)=
[t+
(10-t)-
t]=
,
∴AH=
-
t或
t-
,
在Rt△AEH中,AE2=EH2+AH2,
(
)2+(
)2=(
)2,
∴解得:t1=3,t2=7,
当t=3时,OH=
+
t=4,
∴E点坐标为(4,
),
把E(4,
)代入y=
得k=4×
=10
;
当t=7时,OH=
+
=6,
∴E点坐标为(6,
),
把E(6,
)代入y=
得k=6×
=15
;
综上所述:k的值为10
或15
.
 解:作EH⊥OB于H点,如图,
解:作EH⊥OB于H点,如图,∵E为CD的中点,
∴EH为梯形CMND的中位线,
∴EH=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
5
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴AH=
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
在Rt△AEH中,AE2=EH2+AH2,
(
5
| ||
| 2 |
| 5-t |
| 2 |
| ||
| 2 |
∴解得:t1=3,t2=7,
当t=3时,OH=
| 5 |
| 2 |
| 1 |
| 2 |
∴E点坐标为(4,
5
| ||
| 2 |
把E(4,
5
| ||
| 2 |
| k |
| x |
5
| ||
| 2 |
| 3 |
当t=7时,OH=
| 5 |
| 2 |
| t |
| 2 |
∴E点坐标为(6,
5
| ||
| 2 |
把E(6,
5
| ||
| 2 |
| k |
| x |
5
| ||
| 2 |
| 3 |
综上所述:k的值为10
| 3 |
| 3 |
点评:本题考查了反比例函数的综合题:反比例函数图象上点的坐标满足其函数解析式,运用待定系数法求函数的解析式等知识,用未知数表示出EH,AH的长是解题关键.

练习册系列答案
相关题目
 填空,完成下列说理过程.
填空,完成下列说理过程.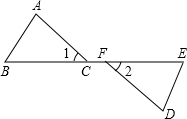 如图,点B、C、F、E在同一直线上,∠1=∠2,BF=EC,要使△ABC≌△DEF,还需添加的一个条件是
如图,点B、C、F、E在同一直线上,∠1=∠2,BF=EC,要使△ABC≌△DEF,还需添加的一个条件是 根据图象回答下列问题.
根据图象回答下列问题.