题目内容
若关于x的一元二次方程ax2+bx+c=0(a≠0)的两根为x1,x2,则x1+x2=-
,x1•x2=
.当a=1,b=6,c=5时,x1x2+x1+x2的值是( )
| b |
| a |
| c |
| a |
| A、5 | B、-5 | C、1 | D、-1 |
考点:根与系数的关系
专题:计算题,整体思想
分析:根据根与系数的关系得到x1+x2=-6,x1•x2=5,然后利用整体代入的方法计算x1x2+x1+x2的值.
解答:解:根据题意得x1+x2=-6,x1•x2=5,
所以x1x2+x1+x2=5-6=-1.
故选D.
所以x1x2+x1+x2=5-6=-1.
故选D.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-
,x1•x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
 如图,在四边形ABCD中,E,F分别为AC,BD的中点,则EF与AB+CD的关系是( )
如图,在四边形ABCD中,E,F分别为AC,BD的中点,则EF与AB+CD的关系是( )| A、2EF=AB+CD |
| B、2EF>AB+CD |
| C、2EF<AB+CD |
| D、不确定 |
已知两圆的半径长是方程x2-10x+24=0的两个解,且两圆的圆心距为d,若两圆相离,则下列结论正确的是( )
| A、0<d<2 |
| B、d>10 |
| C、0≤d<2或d>10 |
| D、0<d<2或d>10 |
 如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠4=70°,则∠3等于( )
如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠4=70°,则∠3等于( )| A、40° | B、50° |
| C、70° | D、80° |
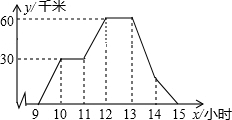 A、B两地相距60千米,图中折线表示某骑车人离A地的距离与时间的函数关系,有一辆客车9时从B地出发,以60千米/小时的速度为匀速行驶,并返往于两地之间(乘客上、下车停留时间忽略不计)
A、B两地相距60千米,图中折线表示某骑车人离A地的距离与时间的函数关系,有一辆客车9时从B地出发,以60千米/小时的速度为匀速行驶,并返往于两地之间(乘客上、下车停留时间忽略不计)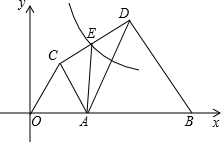 如图,点B的坐标为(10,0),点A是OB上的一个动点,且OA<AB,分别以OA、AB为边在x轴上方作等边三角形OAC和等边三角形ABD,连接CD,E为CD的中点,双曲线y=
如图,点B的坐标为(10,0),点A是OB上的一个动点,且OA<AB,分别以OA、AB为边在x轴上方作等边三角形OAC和等边三角形ABD,连接CD,E为CD的中点,双曲线y=