题目内容
 填空,完成下列说理过程.
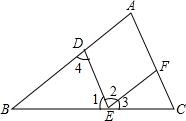
填空,完成下列说理过程.如图,点D、E、F分别在AB、BC、AC上,且DE∥AC,EF∥AB,试说明“∠A+∠B+∠C=180°”
证明:∵DE∥AC (已知)
∴∠1=∠
∵AB∥EF (已知)
∴∠3=∠
∵AB∥EF (已知)
∴∠2=∠
∵DE∥AC (已知)
∴∠4=∠
∵∠2=∠A (等量代换).
∵∠1+∠2+∠3=180°
∴∠A+∠B+∠C=180°(等量代换).
考点:平行线的判定与性质
专题:推理填空题
分析:此题是根据平行线的判定与性质,将求(∠A+∠B+∠C)转化为求(∠1+∠2+∠3)的值.
解答:证明:∵DE∥AC(已知),
∴∠1=∠3.
∵AB∥EF(已知),
∴∠3=∠B.
∵AB∥EF(已知),
∴∠2=∠4(两直线平行,内错角相等).
∵DE∥AC(已知),
∴∠4=∠A(两直线平行,同位角相等).
∵∠2=∠A(等量代换),∠1+∠2+∠3=180°,
∴∠A+∠B+∠C=180°(等量代换).
故答案是:3;B;4;(两直线平行,内错角相等);A;(两直线平行,同位角相等).
∴∠1=∠3.
∵AB∥EF(已知),
∴∠3=∠B.
∵AB∥EF(已知),
∴∠2=∠4(两直线平行,内错角相等).
∵DE∥AC(已知),
∴∠4=∠A(两直线平行,同位角相等).
∵∠2=∠A(等量代换),∠1+∠2+∠3=180°,
∴∠A+∠B+∠C=180°(等量代换).
故答案是:3;B;4;(两直线平行,内错角相等);A;(两直线平行,同位角相等).
点评:本题考查了平行线的判定与性质.此题实际上是利用平行线的判定与性质来证明三角形的内角和是180度.解答此题的关键是注意平行线的性质和判定定理的综合运用.

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,E、F分别是边AB,CD中点,连结EF,DE、BF.
如图,在平行四边形ABCD中,E、F分别是边AB,CD中点,连结EF,DE、BF.
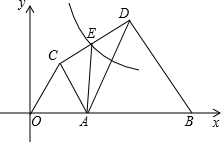 如图,点B的坐标为(10,0),点A是OB上的一个动点,且OA<AB,分别以OA、AB为边在x轴上方作等边三角形OAC和等边三角形ABD,连接CD,E为CD的中点,双曲线y=
如图,点B的坐标为(10,0),点A是OB上的一个动点,且OA<AB,分别以OA、AB为边在x轴上方作等边三角形OAC和等边三角形ABD,连接CD,E为CD的中点,双曲线y=