题目内容
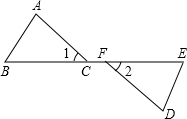 如图,点B、C、F、E在同一直线上,∠1=∠2,BF=EC,要使△ABC≌△DEF,还需添加的一个条件是
如图,点B、C、F、E在同一直线上,∠1=∠2,BF=EC,要使△ABC≌△DEF,还需添加的一个条件是考点:全等三角形的判定
专题:几何图形问题,开放型
分析:此题是一道开放型题目,答案不唯一,可以是AC=DF或∠B=∠E或∠A=∠D(写出其中一个即可).
解答: 可添加的条件为:AC=DF,
可添加的条件为:AC=DF,
证明:∵BF=EC,
∴BF-CF=EC-CF,
即BC=EF,
在△ABC和△DEF中
∴△ABC≌△DEF(SAS),
故答案为:AC=DF.
 可添加的条件为:AC=DF,
可添加的条件为:AC=DF,证明:∵BF=EC,
∴BF-CF=EC-CF,
即BC=EF,
在△ABC和△DEF中
|
∴△ABC≌△DEF(SAS),
故答案为:AC=DF.
点评:本题考查了平行线的性质,全等三角形的判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,题目比较典型,难度适中.

练习册系列答案
相关题目
已知两圆的半径长是方程x2-10x+24=0的两个解,且两圆的圆心距为d,若两圆相离,则下列结论正确的是( )
| A、0<d<2 |
| B、d>10 |
| C、0≤d<2或d>10 |
| D、0<d<2或d>10 |

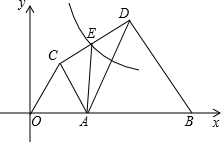 如图,点B的坐标为(10,0),点A是OB上的一个动点,且OA<AB,分别以OA、AB为边在x轴上方作等边三角形OAC和等边三角形ABD,连接CD,E为CD的中点,双曲线y=
如图,点B的坐标为(10,0),点A是OB上的一个动点,且OA<AB,分别以OA、AB为边在x轴上方作等边三角形OAC和等边三角形ABD,连接CD,E为CD的中点,双曲线y=
 阅读理解:对于任意正实数a、b,
阅读理解:对于任意正实数a、b,