题目内容
5.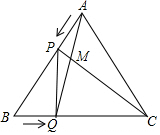 如图,边长为4cm的等边△ABC中,点P、Q分别是边AB、BC上的动点(端点除外),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ,CP交于点M,在点P,Q运动的过程中.
如图,边长为4cm的等边△ABC中,点P、Q分别是边AB、BC上的动点(端点除外),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ,CP交于点M,在点P,Q运动的过程中.(1)求证:△ABQ≌△CAP;
(2)∠QMC的大小是否发生变化?若无变化,求∠QMC的度数;若有变化,请说明理由;
(3)连接PQ,当点P,Q运动多少秒时,△PBQ是直角三角形?
分析 (1)根据等边三角形的性质、三角形全等的判定定理证明;
(2)根据全等三角形的性质得到∠BAQ=∠ACP,根据三角形的外角的性质解答;
(3)分∠PQB=90°和∠PBQ=90°两种情况,根据直角三角形的性质计算即可.
解答 (1)证明:∵△ABC是等边三角形,
∴∠ABQ=∠CAP=60°,AB=CA,
∵点P、Q的速度相同,
∴AP=BQ,
在△ABQ和△CAP中,
$\left\{\begin{array}{l}{AB=CA}\\{∠ABQ=∠CAP}\\{AP=BQ}\end{array}\right.$,
∴△ABQ≌△CAP;
(2)解:∠QMC的大小不发生变化,
∵△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∴∠QMC=∠QAC+∠ACP=∠QAC+∠BAQ=60°;
(3)解:设点P,Q运动x秒时,△PBQ是直角三角形,
则AP=BQ=x,PB=(4-x),
当∠PQB=90°时,
∵∠B=60°,
∴BP=2BQ,即4-x=2x,
解得,x=$\frac{4}{3}$,
当∠PBQ=90°时,
∵∠B=60°,
∴BQ=2BP,即2(4-x)=x,
解得,x=$\frac{8}{3}$,
∴当点P,Q运动$\frac{4}{3}$秒或$\frac{8}{3}$秒时,△PBQ是直角三角形.
点评 本题考查的是全等三角形的判定、直径三角形的性质,掌握等边三角形的性质、灵活运用分情况讨论思想是解题的关键.

练习册系列答案
相关题目
15.由所有到已知点O的距离大于或等于3,并且小于或等于5的点组成的图形的面积为( )
| A. | 4π | B. | 9π | C. | 16π | D. | 25π |
16.为解决群众看病贵的问题,有关部门决定降低药价,对某种原价为100元的药品进行连续两次降价后为81元.设平均每次降价的百分率为x,则下列方程正确的是( )
| A. | 100(1-x)2=81 | B. | 81(1-x)2=100 | C. | 100(1-2x)=81 | D. | 81(1-2x)=100 |
13.-2016的相反数是( )
| A. | -2016 | B. | -$\frac{1}{2016}$ | C. | $\frac{1}{2016}$ | D. | 2016 |
20.若二次根式$\sqrt{1+2x}$有意义,则x的取值范围为 ( )
| A. | x≥$\frac{1}{2}$ | B. | x≥-$\frac{1}{2}$ | C. | x≤$\frac{1}{2}$ | D. | x≤-$\frac{1}{2}$ |
10.下列一组数:-8,2.6,-|-3|,-π,0.101001…(毎两个1中逐次增加一个0)中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17. 如图,△ABC的内切圆O与各边分别相切于点D,E,F,那么下列叙述错误的是( )
如图,△ABC的内切圆O与各边分别相切于点D,E,F,那么下列叙述错误的是( )
 如图,△ABC的内切圆O与各边分别相切于点D,E,F,那么下列叙述错误的是( )
如图,△ABC的内切圆O与各边分别相切于点D,E,F,那么下列叙述错误的是( )| A. | 点O是△ABC的三条角平分线的交点 | |
| B. | 点O是△DEF的三条中线的交点 | |
| C. | 点O是△DEF的三条边的垂直平分线的交点 | |
| D. | △DEF一定是锐角三角形 |
14. 如图,数轴上的点A所表示的数为a,化简|a|+|1-a|的结果为( )
如图,数轴上的点A所表示的数为a,化简|a|+|1-a|的结果为( )
 如图,数轴上的点A所表示的数为a,化简|a|+|1-a|的结果为( )
如图,数轴上的点A所表示的数为a,化简|a|+|1-a|的结果为( )| A. | 1 | B. | 2a-1 | C. | 2a+1 | D. | 1-2a |
15.下列计算结果为a5的是( )
| A. | a2+a3 | B. | a2•a3 | C. | (a3)2 | D. | a15÷a3 |