题目内容
17. 如图,△ABC的内切圆O与各边分别相切于点D,E,F,那么下列叙述错误的是( )
如图,△ABC的内切圆O与各边分别相切于点D,E,F,那么下列叙述错误的是( )| A. | 点O是△ABC的三条角平分线的交点 | |
| B. | 点O是△DEF的三条中线的交点 | |
| C. | 点O是△DEF的三条边的垂直平分线的交点 | |
| D. | △DEF一定是锐角三角形 |
分析 根据切线的性质得到OD⊥AB,OE⊥BC,OF⊥AC,根据同圆的半径相等得到OD=OE=OF,于是得到点O是△ABC的三条角平分线的交点,根据外接圆的圆心的性质得到点O是△DEF的三条边的垂直平分线的交点,根据四边形的内角和和圆周角定理得到DEF是锐角三角形.
解答 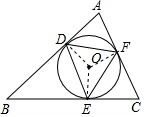 解:连接OD,OE,OF,
解:连接OD,OE,OF,
∵△ABC的内切圆O与各边分别相切于点D,E,F,
∴OD⊥AB,OE⊥BC,OF⊥AC,
∵OD=OE=OF,
∴点O是△ABC的三条角平分线的交点,
∵⊙O是△DEF的外接圆,
∴点O是△DEF的三条边的垂直平分线的交点,
∵∠ADO=∠AFO=90°,
∴∠A+∠DOF=180°,
∴∠DOF=180°-∠A,
∴∠DEF=$\frac{1}{2}$∠DOF=90°-$\frac{1}{2}∠$A,
∴∠DEF是锐角,同理∠EDF与∠DFE是锐角,
∴△DEF是锐角三角形,
故选B.
点评 此题主要考查了三角形的内心与外心的性质;三角形的内心:三条角平分线的交点,到三角形三边的距离相等;三角形的外心:三边中垂线的交点,到三角形三个顶点的距离相等.

练习册系列答案
相关题目
7.-2017的绝对值是( )
| A. | 2017 | B. | -2017 | C. | $\frac{1}{2017}$ | D. | -$\frac{1}{2017}$ |
2.从3,-1,$\frac{1}{2}$,1,-3这5个数中,随机抽取一个数记为a,若数a使关于x的不等式组$\left\{\begin{array}{l}{\frac{1}{3}(2x+7)≥3}\\{x-a<0}\end{array}\right.$无解,且使关于x的分式方程$\frac{x}{x-3}$-$\frac{a-2}{3-x}$=-1有整数解,那么这5个数中所有满足条件的a的值之积是( )
| A. | $\frac{1}{2}$ | B. | 3 | C. | -3 | D. | -$\frac{3}{2}$ |
9. 如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=30°,则∠CAB=( )
如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=30°,则∠CAB=( )
 如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=30°,则∠CAB=( )
如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=30°,则∠CAB=( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
6.下列由左到右的变形,属于因式分解的是( )
| A. | (x+2)(x-2)=x2-4 | B. | x2-4=(x+2)(x-2) | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | x2+4x-2=x(x+4)-2 |
7.当式子|x-1|+|x-2|+|x-3|+…+|x-9|取得最小值时,实数x的值等于( )
| A. | 1 | B. | 5 | C. | 6 | D. | 9 |
 如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.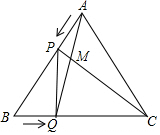 如图,边长为4cm的等边△ABC中,点P、Q分别是边AB、BC上的动点(端点除外),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ,CP交于点M,在点P,Q运动的过程中.
如图,边长为4cm的等边△ABC中,点P、Q分别是边AB、BC上的动点(端点除外),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ,CP交于点M,在点P,Q运动的过程中.