题目内容
14. 如图,数轴上的点A所表示的数为a,化简|a|+|1-a|的结果为( )
如图,数轴上的点A所表示的数为a,化简|a|+|1-a|的结果为( )| A. | 1 | B. | 2a-1 | C. | 2a+1 | D. | 1-2a |
分析 根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简,合并即可得到结果.
解答 解:根据数轴上点的位置得:1<a<2,
∴1-a<0,
则原式=a+a-1=2a-1,
故选B
点评 此题考查了整式的加减,数轴,以及绝对值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
4.单项式-$\frac{2abc}{3}$的系数和次数分别是( )
| A. | -$\frac{2}{3}$,3 | B. | -$\frac{2}{3}$,1 | C. | -2,3 | D. | -2,1 |
2.从3,-1,$\frac{1}{2}$,1,-3这5个数中,随机抽取一个数记为a,若数a使关于x的不等式组$\left\{\begin{array}{l}{\frac{1}{3}(2x+7)≥3}\\{x-a<0}\end{array}\right.$无解,且使关于x的分式方程$\frac{x}{x-3}$-$\frac{a-2}{3-x}$=-1有整数解,那么这5个数中所有满足条件的a的值之积是( )
| A. | $\frac{1}{2}$ | B. | 3 | C. | -3 | D. | -$\frac{3}{2}$ |
9. 如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=30°,则∠CAB=( )
如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=30°,则∠CAB=( )
 如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=30°,则∠CAB=( )
如图,C,D是以线段AB为直径的⊙O上两点,若CA=CD,且∠ACD=30°,则∠CAB=( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
6.下列由左到右的变形,属于因式分解的是( )
| A. | (x+2)(x-2)=x2-4 | B. | x2-4=(x+2)(x-2) | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | x2+4x-2=x(x+4)-2 |
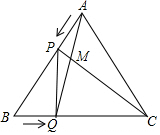 如图,边长为4cm的等边△ABC中,点P、Q分别是边AB、BC上的动点(端点除外),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ,CP交于点M,在点P,Q运动的过程中.
如图,边长为4cm的等边△ABC中,点P、Q分别是边AB、BC上的动点(端点除外),点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ,CP交于点M,在点P,Q运动的过程中.
 如图,在△ABC中,∠ACB=Rt∠,BC=6,AC=8,点D是AC的中点,点P为AB边上的动点(P不与A重合),AP=t(t>0),PH⊥AC于点H,则PH=$\frac{3}{5}$t,连结DP并延长至点E,使得PE=PD,作点E关于AB的对称点F,连结FH
如图,在△ABC中,∠ACB=Rt∠,BC=6,AC=8,点D是AC的中点,点P为AB边上的动点(P不与A重合),AP=t(t>0),PH⊥AC于点H,则PH=$\frac{3}{5}$t,连结DP并延长至点E,使得PE=PD,作点E关于AB的对称点F,连结FH