题目内容
16．
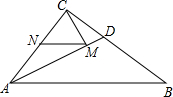如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AD是Rt△ABC的角平分线，若点M、N分别是线段AD和边AC上的动点，则MC+MN的最小值是$\frac{24}{5}$．
分析 首先过点C作CE⊥AB交AB于点E，交AD于点M，过点M作MN⊥AC于点N，由AD是∠BAC的平分线．得出MN=ME，可得此时MC+MN有最小值，即CE的长度，运用勾股定理求出AB，再运用S△ABC=$\frac{1}{2}$AB•CE=$\frac{1}{2}$AC•BC，得出CE的值，即MC+MN的最小值．
解答 
解：如图，过点C作CE⊥AB交AB于点E，交AD于点M，过点M作MN⊥AC于点N，
∵AD是∠BAC的平分线．
∴MN=ME，则此时MC+MN有最小值，即CE的长度，
∵AC=6，BC=8，∠ACB=90°，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10．
∵S△ABC=$\frac{1}{2}$AB•CE=$\frac{1}{2}$AC•BC，
∴CE=$\frac{AC•BC}{AB}$=$\frac{24}{5}$，
即MC+MN的最小值为$\frac{24}{5}$．
故答案为：$\frac{24}{5}$．
点评 此题考查了最短路径问题．注意准确找到点M与N的位置是解此题的关键．
练习册系列答案
相关题目
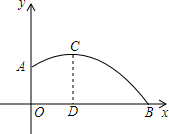如图所示，一男生推铅球，铅球在点A处出手，出手时铅球离地面$\frac{5}{3}$m．铅球落地点在B处，铅球运行中在该男生前4m处（即0D=4）达到最高点，此时铅球离地面3m．根据图示的直角坐标系，你能算出该男生推铅球的成绩吗？
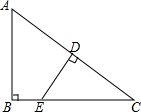如图，在Rt△ABC中，∠ABC=90°，AB=6，BC=8，点D是AC中点，过点D作DE⊥AC交BC于点E，则CE的长度是$\frac{25}{4}$．
一个长方体的三视图如图所示．若其俯视图为正方形，求这个长方体的表面积．