题目内容
6.直线y=-x-2与y=x+3的交点在第二象限.分析 联立两直线解析式,解关于x、y的二元一次方程组,再根据各象限内点的坐标特征解答.
解答 解:联立$\left\{\begin{array}{l}{y=-x-2}\\{y=x+3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-\frac{5}{2}}\\{y=\frac{1}{2}}\end{array}\right.$,
所以,交点坐标为(-$\frac{5}{2}$,$\frac{1}{2}$),在第二象限.
故答案为:第二.
点评 本题考查了两直线相交的问题,联立直线解析式求交点坐标是常用的方法,要熟练掌握并灵活运用.

练习册系列答案
相关题目
15.下列等式的变形正确的是( )
| A. | 如果x+2=y,那么x=y+2 | B. | 如果$\frac{1}{3}$x=9,那么x=3 | ||
| C. | 如果x=y,那么ax=ay | D. | 如果x=y,那么$\frac{x}{a}$=$\frac{y}{a}$ |
 如图,AB=AC,要使△ABE≌△ACD,依据ASA,应添加的一个条件是∠C=∠B.
如图,AB=AC,要使△ABE≌△ACD,依据ASA,应添加的一个条件是∠C=∠B.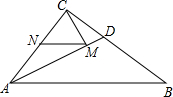 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是Rt△ABC的角平分线,若点M、N分别是线段AD和边AC上的动点,则MC+MN的最小值是$\frac{24}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是Rt△ABC的角平分线,若点M、N分别是线段AD和边AC上的动点,则MC+MN的最小值是$\frac{24}{5}$.