题目内容
1.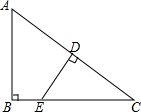 如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点D是AC中点,过点D作DE⊥AC交BC于点E,则CE的长度是$\frac{25}{4}$.
如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点D是AC中点,过点D作DE⊥AC交BC于点E,则CE的长度是$\frac{25}{4}$.
分析 根据勾股定理得到AC=10,由DE⊥AC于D,得到∠ADE=90°,推出△CED∽△ACB,根据相似三角形的性质即可得到结论.
解答 解:∵∠ABC=90°,AB=6,BC=8,
∴AC=10,
∵DE⊥AC于D,
∴∠ADE=90°,
∵∠C=∠C,
∴△CED∽△ACB,
∴CD:CB=CE:AC,
∵D是AC中点,
∴CD=5,
∴5:8=CE:10,
∴CE=$\frac{25}{4}$.
故答案为:$\frac{25}{4}$.
点评 本题考查了勾股定理的运用以及相似三角形的判定和性质,垂直的定义,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
9.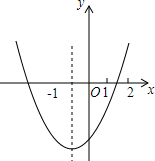 对称轴为直线x=-1的抛物线y=ax2+bx+c如图所示,有下列结论:
对称轴为直线x=-1的抛物线y=ax2+bx+c如图所示,有下列结论:
①abc<0;②16a-4b+c<0;③ax2+bx≥a-b;④3a+c<0.
其中,正确结论的个数是( )
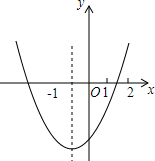 对称轴为直线x=-1的抛物线y=ax2+bx+c如图所示,有下列结论:
对称轴为直线x=-1的抛物线y=ax2+bx+c如图所示,有下列结论:①abc<0;②16a-4b+c<0;③ax2+bx≥a-b;④3a+c<0.
其中,正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.从六边形的一个顶点作对角线,把这个六边形分成三角形的个数是( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6 个 |
 如图,AB=AC,要使△ABE≌△ACD,依据ASA,应添加的一个条件是∠C=∠B.
如图,AB=AC,要使△ABE≌△ACD,依据ASA,应添加的一个条件是∠C=∠B.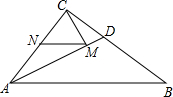 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是Rt△ABC的角平分线,若点M、N分别是线段AD和边AC上的动点,则MC+MN的最小值是$\frac{24}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是Rt△ABC的角平分线,若点M、N分别是线段AD和边AC上的动点,则MC+MN的最小值是$\frac{24}{5}$. 已知,如图:AD、BC相交于点O,AD=BC,∠C=∠D=90°.求证:AO=BO,CO=DO.
已知,如图:AD、BC相交于点O,AD=BC,∠C=∠D=90°.求证:AO=BO,CO=DO.