题目内容
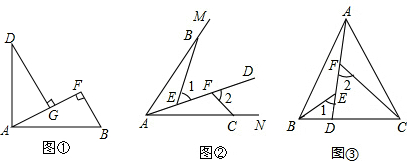
4.感知:如图①.AB=AD,AB⊥AD,BF⊥AF于点F,DG⊥AF于点G.求证:△ADG≌△BAF.拓展:如图②,点B、C在∠MAN的边AM、AN上,点E、F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角,已知AB=AC,∠1=∠2=∠BAC.
应用:如图③,在△ABC中,AB=AC,AB>BC,点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为12,则△ABE与△CDF的面积之和为8.
分析 感知:利用AAS证明△ADG≌△BAF;
拓展:利用∠1=∠2=∠BAC,利用三角形外角性质得出∠4=∠ABE,进而利用AAS证明△ABE≌△CAF;
应用:首先根据△ABD与△ADC等高,底边比值为:1:2,得出△ABD与△ADC面积比为:1:2,再证明△ABE≌△CAF,即可得出△ABE与△CDF的面积之和为△ADC的面积得出答案即可.
解答 解:感知:
∵AB⊥AD,BF⊥AF,DG⊥AF,
∴∠DGA=∠BFA=∠DAB=90°,
∴∠DAG+∠FAB=90°,.
∠B+∠FAB=90°,
∴∠B=∠DAG,
在△ADG和△BAF中,
$\left\{\begin{array}{l}{∠B=∠DAG}\\{∠AFB=∠DGA}\\{AB=AD}\end{array}\right.$
∴△ADG≌△BAF.
拓展:如图②,
:∵∠1=∠2,
∴∠BEA=∠AFC,
∵∠1=∠ABE+∠3,∠3+∠4=∠BAC,∠1=∠BAC,
∴∠BAC=∠ABE+∠3,
∴∠4=∠ABE,
在△ABE和△CAF中,
$\left\{\begin{array}{l}{∠AEB=∠AFC}\\{∠ABE=∠4}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△CAF(AAS).
应用如图③,
∵在等腰三角形ABC中,AB=AC,CD=2BD,
∴△ABD与△ADC等高,底边比值为:1:2,
∴△ABD与△ADC面积比为:1:2,
∵△ABC的面积为12,
∴△ABD与△ADC面积分别为:4,8;
∵∠1=∠2,
∴∠BEA=∠AFC,
∵∠1=∠ABE+∠3,∠3+∠4=∠BAC,∠1=∠BAC,
∴∠BAC=∠ABE+∠3,
∴∠4=∠ABE,
∴在△ABE和△CAF中,
$\left\{\begin{array}{l}{∠AEB=∠AFC}\\{∠ABE=∠4}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△CAF(AAS),
∴△ABE与△CAF面积相等,
∴△ABE与△CDF的面积之和为△ADC的面积,
∴△ABE与△CDF的面积之和为8,
故答案为:8.
点评 此题主要考查了三角形全等的判定与性质以及三角形面积求法,根据已知得出∠4=∠ABE,以及△ABD与△ADC面积比为:1:2是解题关键.

| A. | 如果x+2=y,那么x=y+2 | B. | 如果$\frac{1}{3}$x=9,那么x=3 | ||
| C. | 如果x=y,那么ax=ay | D. | 如果x=y,那么$\frac{x}{a}$=$\frac{y}{a}$ |
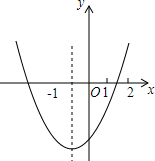 对称轴为直线x=-1的抛物线y=ax2+bx+c如图所示,有下列结论:
对称轴为直线x=-1的抛物线y=ax2+bx+c如图所示,有下列结论:①abc<0;②16a-4b+c<0;③ax2+bx≥a-b;④3a+c<0.
其中,正确结论的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6 个 |
| A. | 两个不相等的实数根 | B. | 两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
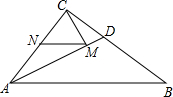 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是Rt△ABC的角平分线,若点M、N分别是线段AD和边AC上的动点,则MC+MN的最小值是$\frac{24}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是Rt△ABC的角平分线,若点M、N分别是线段AD和边AC上的动点,则MC+MN的最小值是$\frac{24}{5}$.