题目内容
9.二次函数y=-x2-2x+3的图象与x轴交于A、B两点(A在B的左边),它的顶点为C点.连接AC、BC,则tan∠CAB的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | 2 |
分析 利用待定系数法求出A、B、C三点坐标,设对称轴交x轴于D,在Rt△ACD中,∠ADC=90°,AD=2,CD=4,根据tan∠CAB=$\frac{CD}{AD}$,计算即可.
解答 解:对于抛物线y=-x2-2x+3,令y=0,得-x2-2x+3=0,解得x=-3或1,
∴A(-3,0),B(1,0),
∵y=-x2-2x+3=-(x+1)2+4,
∴顶点C(-1,4),如图,设对称轴交x轴于D.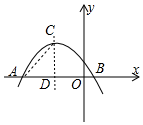
在Rt△ACD中,∠ADC=90°,AD=2,CD=4,
∴tan∠CAB=$\frac{CD}{AD}$=2,
故选D.
点评 本题考查抛物线与x轴的交点、解直角三角形等知识,解题的关键是灵活运用所学知识,学会用转化的思想思考问题,学会添加常用辅助线,构造直角三角形解决问题.

练习册系列答案
相关题目
4. 如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=-1是对称轴,有下列判断:①b-2a=0,②4a-2b+c<0,③a-b+c=-9a,④若(-3,y1),($\frac{3}{2}$,y2)是抛物线上的两点,则y1<y2.其中正确的是( )
如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=-1是对称轴,有下列判断:①b-2a=0,②4a-2b+c<0,③a-b+c=-9a,④若(-3,y1),($\frac{3}{2}$,y2)是抛物线上的两点,则y1<y2.其中正确的是( )
 如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=-1是对称轴,有下列判断:①b-2a=0,②4a-2b+c<0,③a-b+c=-9a,④若(-3,y1),($\frac{3}{2}$,y2)是抛物线上的两点,则y1<y2.其中正确的是( )
如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=-1是对称轴,有下列判断:①b-2a=0,②4a-2b+c<0,③a-b+c=-9a,④若(-3,y1),($\frac{3}{2}$,y2)是抛物线上的两点,则y1<y2.其中正确的是( )| A. | ①②③ | B. | ①③ | C. | ①④ | D. | ①③④ |
19.下列说法中正确的是( )
| A. | 含有一个未知数的等式是一元一次方程 | |
| B. | 未知数的次数都是1次的方程是一元一次方程 | |
| C. | 含有一个未知数,并且未知数的次数都是一次的方程是一元一次方程 | |
| D. | 2t-7=1是一元一次方程 |
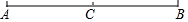 已知:如图,线段AB=10,C是AB的中点.
已知:如图,线段AB=10,C是AB的中点.