题目内容
18．解方程4（x-1）-x=2（x+$\frac{1}{2}$）步骤如下：①去括号，得4x-4-x=2x+1；②移项，得4x+x-2x=4+1；③合并同类项，得3x=5；④化系数为1，x=$\frac{5}{3}$．其中错误的一步是（ ）| A． | ① | B． | ② | C． | ③ | D． | ④ |
分析 根据移项可得4x-x-2x=4+1，因此②错误．
解答 解：4（x-1）-x=2（x+$\frac{1}{2}$），
去括号，得4x-4-x=2x+1，
移项，得4x-x-2x=4+1，
合并同类项，得x=5，
错误的一步是②，
故选：B．
点评 此题主要考查了解一元一次方程，关键是正确掌握一元一次方程的解法，注意移项要变号．
练习册系列答案
相关题目
8．
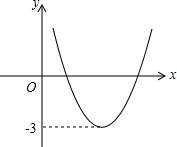如图，已知函数y=ax2+bx+c的图象如图所示，那么关于x的方程ax2+bx+c+2=0的根的情况是（ ）
如图，已知函数y=ax2+bx+c的图象如图所示，那么关于x的方程ax2+bx+c+2=0的根的情况是（ ）| A． | 有两个同号不相等的实数根 | B． | 有两个异号实数根 | ||
| C． | 有两个相等实数根 | D． | 无实数根 |
9．二次函数y=-x2-2x+3的图象与x轴交于A、B两点（A在B的左边），它的顶点为C点．连接AC、BC，则tan∠CAB的值是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{5}}{5}$ | C． | $\frac{2\sqrt{5}}{5}$ | D． | 2 |
13．下列算式能用平方差公式计算的是（ ）
| A． | （3a+b）（3b-a） | B． | （$\frac{1}{3}$x-1）（1+$\frac{1}{3}$x） | C． | （2x-y）（-2x+y） | D． | （-s-t）（-s-t） |
10．下列事件中，不可能事件是（ ）
| A． | 掷一枚均匀的正方形骰子，朝上一面的点数是5 | |
| B． | 任意选择某个电视频道，正在播放动画片 | |
| C． | 明天太阳从西边升起 | |
| D． | 抛出一枚硬币，落地后正面朝上 |
7．在△ABC与△A′B′C′中，已知∠A=∠A′，AC=A′C′，下列说法错误的是（ ）
| A． | 若添加条件AB=A′B′，则△ABC≌△A′B′C′ | |
| B． | 若添加条件∠C=∠C′，则△ABC≌△A′B′C′ | |
| C． | 若添加条件∠B=∠B′，则△ABC≌△A′B′C′ | |
| D． | 若添加条件BC=B′C′，则△ABC≌△A′B′C′ |
