题目内容
19.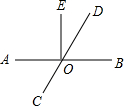 如图,直线AB,CD相交于点O,OE⊥AB,O为垂足,∠EOD=30°,则∠AOC=60°.
如图,直线AB,CD相交于点O,OE⊥AB,O为垂足,∠EOD=30°,则∠AOC=60°.
分析 首先根据OE⊥AB,可得∠EOB=90°,然后根据∠EOD=30°,求出BOD的度数,再根据对顶角相等,即可判断出∠AOC的度数是多少.
解答 解:∵OE⊥AB,
∴∠EOB=90°,
∵∠EOD=30°,
∴BOD=90°-30°=60°,
∵∠AOC=∠BOD,
∴∠AOC=60°.
故答案为:60°.
点评 (1)此题主要考查了垂线的性质和应用,要熟练掌握,解答此类问题的关键是要明确:垂线的性质在平面内,过一点有且只有一条直线与已知直线垂直.
(2)此题还考查了对顶角的特征和性质的应用,要熟练掌握,解答此题的关键是要明确:对顶角相等.

练习册系列答案
相关题目
4.为了帮助农村贫困家庭子女完成初中学业,国家给他们免费提供教科书,下表是某中学免费提供教科书补助的部分情况:
求获得免费提供教科书补助的七年级和八年级的人数.
| 年级 项目 | 七 | 八 | 九 | 合计 |
| 每人免费补助金额/元 | 109 | 94 | 47.5 | - |
| 人数/人 | 40 | 120 | ||
| 免费补助金额/元 | 1900 | 10095 |
11.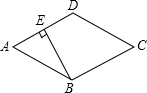 如图,已知菱形ABCD的边长为4,∠ABC=120°,过B作BE⊥AD,则BE的长为( )
如图,已知菱形ABCD的边长为4,∠ABC=120°,过B作BE⊥AD,则BE的长为( )
 如图,已知菱形ABCD的边长为4,∠ABC=120°,过B作BE⊥AD,则BE的长为( )
如图,已知菱形ABCD的边长为4,∠ABC=120°,过B作BE⊥AD,则BE的长为( )| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 1 |
 如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.(画出图形并写出解答过程)
如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.(画出图形并写出解答过程) 已知2y-3与-3x-1成正比例,且x=2时,y=5.
已知2y-3与-3x-1成正比例,且x=2时,y=5.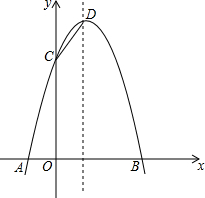 如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).