题目内容
1.(1)计算:$\sqrt{12}$+$\sqrt{6}$×$\sqrt{\frac{1}{2}}$-$\frac{\sqrt{54}}{\sqrt{2}}$(2)计算:3$÷\sqrt{3}$×$\frac{1}{\sqrt{3}}$+(2-$\sqrt{3}$)×$(2+\sqrt{3})$.
分析 (1)先根据二次根式的乘除法则运算得到原式=2$\sqrt{3}$+$\sqrt{6×\frac{1}{2}}$-$\sqrt{\frac{54}{2}}$,然后化简后合并即可;
(2)先根据二次根式的乘除法则和平方差公式计算,然后合并即可.
解答 解:(1)原式=2$\sqrt{3}$+$\sqrt{6×\frac{1}{2}}$-$\sqrt{\frac{54}{2}}$
=2$\sqrt{3}$+$\sqrt{3}$-3$\sqrt{3}$
=0;
(2)原式=3×$\frac{1}{\sqrt{3}}$×$\frac{1}{\sqrt{3}}$+4-3
=1+1
=2.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
13.下列分式中,无论x取什么值,总有意义的是( )
| A. | $\frac{1}{{x}^{2}+1}$ | B. | $\frac{x}{2x+1}$ | C. | $\frac{1}{{x}^{2}}$ | D. | $\frac{x-5}{x}$ |
11.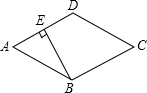 如图,已知菱形ABCD的边长为4,∠ABC=120°,过B作BE⊥AD,则BE的长为( )
如图,已知菱形ABCD的边长为4,∠ABC=120°,过B作BE⊥AD,则BE的长为( )
 如图,已知菱形ABCD的边长为4,∠ABC=120°,过B作BE⊥AD,则BE的长为( )
如图,已知菱形ABCD的边长为4,∠ABC=120°,过B作BE⊥AD,则BE的长为( )| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 1 |
 如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.(画出图形并写出解答过程)
如图,已知△ABC和点O,画出△DEF,使△DEF和△ABC关于点O成中心对称.(画出图形并写出解答过程)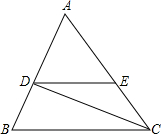 已知:如图,CD是∠ACB的平分线,∠ACB=48°,∠BDC=82°,DE∥BC.
已知:如图,CD是∠ACB的平分线,∠ACB=48°,∠BDC=82°,DE∥BC.